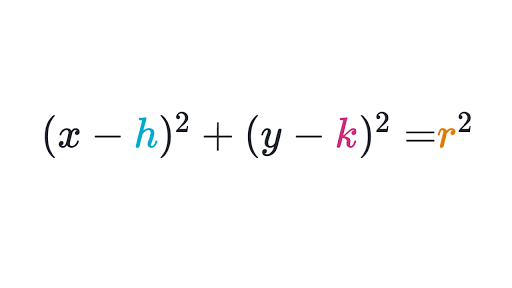So, once you get up in middle school, your long journey with algebra starts. If you are a math lover, algebra is going to interest you because in the long run no matter wherever you go, everything is based on algebra. Moreover, if you are just a simple science student or want to pursue it later, you simply cannot deny algebra. Be it math, physics, chemistry, statistics, economics no matter wherever you go, you will find it. However, as a beginner algebra might be a little confusing since it is very different from normal arithmetic sums. So, in algebra, we form equations with constants and variables depending on the information that we already have and the values that we need to find out. Therefore, the concept of polynomials comes in. If you want to learn about completing the square calculator, you need to know about polynomials first.

So, a polynomial is an algebraic expression where you have several terms. However, the same variable might have different powers in each term. Therefore, if the maximum power of the unknown variable is 2, it is a quadratic polynomial. On the other hand, if the maximum power of the unknown variable is 3, it is a cubic polynomial. Moreover, if it has power to the 4th degree, it is a quartic polynomial and it goes on this way. However, about completing the square calculator we will only need the quadratic polynomial.

Read Also:Double Integral Calculator: Definition, Examples

Hence, completing the square calculator is something that you use when you want to solve a quadratic equation. So, you try to solve it by transforming it into either an addition or a subtraction of a perfect square. We will see how in the ensuing sections of the article.

Completing the square calculator formula

So, we have already seen that for completing the square calculator, the most basic requirement is a quadratic polynomial. Therefore, now let us take a quick look at the formula that it uses for a better understanding of its working.

So, the basic formula is ax^2 + bx + c => a (x + m)^2 + n. Here both ‘m’ and ‘n’ are real numbers. However, let us try to understand what this means exactly. So, the quadratic polynomial is ax^2 + bx + c. Therefore, the unknown variable here is x with coefficients a and b. C is the constant term. So, we can do middle-term factorization of a quadratic equation. However, if both the factors are the same, we can easily write it in a whole square form.

Now, coming back, such a perfect square is not always possible. So, completing the square calculator uses the “a (x + m)^2 + n” formula. Now, the (x + m)^2 is the whole square part. However, inside it, it can either be x + m or x – n depending on the mother polynomial.

So, in short, it is a formula that will help you to convert a quadratic polynomial or equation into a perfect square by adding some constant.

Completing the square calculator Symbolab

The internet has made everything very easy these days. Whatever you need, you get it almost instantly. So, on one hand, we have become restless and engage our brains less but on the brighter side, we get to know about a lot of things very easily. Similarly, you can use completing the square calculator. If you still have difficulty understanding how you can solve such a sum, go for it. Moreover, the calculator will show you stepwise the calculation such that you understand it better. Or if the situation arises that you cannot solve a particular problem, the calculator is always there. However, once you have learned it, you might still need it. Suppose you want to verify an answer that you have manually found, you can go for it because often manual workouts are incorrect.

There are many completing square calculators that we can find online. However, in this article, we will stick to the calculator from Symbolab. So, now we will go through the steps that will help us to operate the calculator by ourselves.

Completing the square calculator with steps

So, for completing the square calculator, you will need to follow several steps correctly. Therefore, let us take a look at them one by one. Make sure that you miss no step in the middle of the answer you get will be incorrect.

Step 1 for completing the square calculator

At first, you have to reach the Symbolabs by completing the square calculator. So, click Symbolab here and you will land directly on the calculator. Now, once you have landed on the page, you will find several sections. At the top, there are a lot of tools that you can use for various mathematical calculations. So right below that, you have a box that looks like a search engine. It reads “complete the square”. This is where you will have to type your data. Once you have typed your data, the solutions section will come below it. However, before doing so, you will find an option of examples where you can find probable examples to see the calculation even when you do not have a question of your own.

Step 2 for completing the square calculator

So, now you have to enter your data in the box that looks like a search engine. Let us say, our polynomial is x^2 + 3x. So, we have a quadratic expression but we do not have the constant term here. Now, there is a button right beside the box that reads “go” and is red. So, click it.

Step 3 for completing the square calculator

Now, completing the square calculator will take a few seconds to run your program, and then you will find the stepwise solving of your sum in the solutions section. So, let us take a look at the solution to this particular sum.

Therefore, we know if we expand (a + x)^2, we get a^2 + 2ax + x^2.

In this process, we have to ultimately convert the quadratic polynomial into its whole square form. So, we have to write x^2 + 3x in the form of a^2 + 2ax + x^2.

Therefore, by this 2a = 3. Or, we can say a = 3/2

Now, in the next step, we have to both add and then subtract (3/2)^2.

So, now we have the equation that looks like this-

x^2 + 3x + (3/2)^2 – (3/2)^2

Now, if (a + x)^2, we get a^2 + 2ax + x^2, x^2 + 3x + (3/2)^2 must be (x + 3/2)^2

Therefore, we can write the original equation as-

(x + 3/2)^2 – (3/2)^2.

So, completing the square form of x^2 + 3x is (x + 3/2)^2 – (3/2)^2.

However, we can further simplify it. This comes to be (x + 3/2)^2 – 9/4.

Step 4 for completing the square calculator

So now our sum is completely done. However, it might so happen that you have a different answer and are not satisfied with the answer that the calculator has given. Therefore, for that, you have another panel that looks like a search engine right below the solution section. Type in our answer there. So then you find a red button beside it that says “verify”. Click it and you will get to know if your answer is correct or a possible option.

However, there is more than that just. The calculator also allows you to practice quadratic equations which is essential before you start completing the square calculator. Click the option above the verification box and there you go!

Completing the square calculator finding c

In completing the square calculator, you might need to find the c in some cases. However, there is a simple way of doing this. Let us see how with an example.

Suppose the expression is x^2 + 9x + c.

So, you know that the form of a quadratic polynomial is ax^2 + bx + c.

Now, to complete the square, we take out b, divide it by 2 and square it. This is the term c. Therefore, in this case, c is (9/2)^2 or 81/4.

Now, if you want to complete the square, you have (x + 9/2)^2 – 81/4. So no matter what sum you are solving to complete the square, this is how you should always find the term “c”.

Now, if you think dividing the coefficient of x by 2 makes sense because, in the whole square expansion, you will have 2axc. So, the two 2s will cancel each other. Moreover, you need to subtract – 81/4 since you are adding it to make a perfect square. It was not there in the original equation.

Completing the square calculator vertex form

We already know that the quadratic form of an equation is ax^2 + bx + c = y. So now let us take a quick look at the vertex form. This is y = a (x – h)^2 + k.

So, you do realize that the answer essentially remains the same for the example that we have already seen in completing the square calculator. Let us consider the same example.

Therefore, we have (x + 3/2)^2 – 9/4. Now, from here, we can find the vertices of the curve. So, these would be -3/2 and -9/4 because, from the equation, the two vertices are h and k.

The y-intercept will be y(0, 0). Moreover, the zeroes will be at X₁(-3, 0) and X₂(0, 0).

Completing the square calculator fraction

Hence, it might so happen that you have a fraction in your quadratic polynomial. This means either one of the three terms is a fraction- either a coefficient of x or the constant. However, once you feed the expression into completing the square calculator, there is no difference at all. The only thing that you have to do is to arrange it in a way such that there is a whole square form and there is a constant outside it. So, what might happen is one of the terms in the whole square can be a fraction which is fine. Hence, there is no other difference in the process of solving the entire sum. We will do as we have seen before.

Completing the square calculator circle

So let us take an example 4x^2 + 4y^2 – 24x + 32y – 4 = 0

Therefore, this one is a little different because we have two variables here- both x and y. Now you see the squared terms have the same coefficients. So, this is a quadratic equation but it is also the equation of a circle. Now, we will divide the entire equation by 4 to get unitary squared terms. So, we have-

x^2 + y^2 – 6x + 8y – 1 = 0

Therefore, the next step in completing the square calculator will be to group the same terms. So, we can write-

x^2 – 6x + y^2 + 8y – 1 = 0.

Hence, now we will try to form the whole square format of each variable. Therefore, we have-

( x^2 – 6x + 3^2) + (y^2 + 8y + 4^2) – 1 = 3^2 + 4^2

So, we have added 3^2 and 4^2 on both sides to form the whole squares.

Therefore, the final equation comes to be-

(x – 3)^2 + (y + 4)^2 = 25.

Completing the square calculator FAQs

What is the purpose of completing the square?

Ans. So, the reason that we use such a calculator is to find the maximum or minimum values of any quadratic equation. Moreover, we can also use completing the square calculator to simplify or factorize algebraic expressions.

Does completing the square method always work?

Ans. So yes, completing the square method will work under every circumstance. Therefore, it is different from normal factorization which might not always work.

What number should you add to complete the square?

Ans. Well, you have to add a constant to complete the square. The constant depends on the permutation- the combination you have done to form the perfect square.

When completing the square does not work?

Ans. So, there is one prerequisite for completing the square method. For this, the lead coefficient must be 1 or you have to make it so by division.

What quantity should be added to both sides of this equation to complete the square x^2 + 4x – 96?

Ans. The number to be added to both sides is 4. To know how this happens, scroll above and check out completing the square calculator with steps section.