Derivative of sec x

Sec x is another way of writing 1/cos x. Now we need to apply the quotient rule. The quotient rule is that y dash equals (vu dash – uv dash) / v^2 divided by v square. In this case, we have y equals to sec x. However, we are going to let u equal the numerator of 1 and v equal the denominator: cos x. Then after applying the quotient rule, we have v, cos remains unchanged and multiply by u.

So the derivative of 1, the constant, is zero. Then minus u, which is one, times the derivative, and that is the derivative of cos x. Now that is equal to minus sin x all over v^2, which is cos^2 x. Then the result is positive sin x divided by the cos ^2 x. Now rewrite this as [sin x/cos x] times 1/cos x. However, the sin x divided by cos square x is equal to the tangent of x. Also, the 1/cos x is equal to the secant of x. So. the derivative of sec x is equal to the tan x multiplied by sec x.

So, we have f(x) = 1/cos x = u/v

By quotient rule,

f'(x) = (vu’ – uv’) / v2

Now, f'(x) = [cos x d/dx(1) – 1 d/dx(cos x)] / (cos x)2

= [cos x (0) – 1 (-sin x)] / cos2x

= (sin x) / cos2x

= 1/cos x · (sin x)/(cos x)

= sec x · tan x

Derivative of sec x tan x

We have the derivative of the secant of x times the tangent of x plus the secant of x times the derivative of the tangent of x. Next, we need to apply the product rule, and the rule is f times the g. The f function is the secant x, and g is equal to tangent x. Now, f dash is equal to secant x times tangent x. Also, g dash is equal to secant square x. Now we are going to pair things up, y dash is equal to secant x times secant squared x plus tangent x times secant x tangent x. Next, we need to simplify this expression. Now we put the secant x to the front. Then secant x times secant squared x plus tangent square x. This is the result of sec x tan x.

y=sec x tan x

By product rule, f= secx, g=sec^2x and f dash= secx tanx, g dash= sec^2x

Next, y dash= sec x⋅sec^2 x + tan x⋅sec x tan x

Next, y dash= sec x (sec^2 x + tan^2 x)

Derivative of sec square x

Let, sec x is equal to y. Now the derivative of sec squared x equals the derivative y square. Then the derivative of y square’s result is the derivative of 2y. Now, we have y equals sec x. After applying this, we get 2 sec x times derivative of sec x, which is equal to 2sec x times sec x tan x. At last, the derivative of sec square x is 2 sec squared x times tan x.

Let, y = sec x.

By power rule and chain rule, y'(x) = 2 secx d/dx (sec x)

Next, y'(x)= 2 sec x · (sec x · tan x)

Next, y'(x)= 2 sec2x tan x

Derivative of sec x degree

We have the derivative of sec x degree. So, y is equal to sec x degree. However, we know the pi value is 180 degrees. Then x degree equals (π/180)x radians. So, y equals sec (π/180) x. Now the derivative of y is equal to the sec of (π/180) times tan of (π/180) times (π/180). Then the derivative of sec x degree is (π/180) sec x degree times tan x degree.

y = sec x degree

We know π radian = 180 degree

X degree = (π/180)x radians

So y = sec (π/180)x

dy/dx = sec (π/180)x tan (π/180)x (π/180)

= (π/180) sec xo tan x0

Derivative of tan^2 x

We have the derivative of tan square x. So, let y be equal to tan square x. Differentiate with respect to x, dy upon dx equals the derivative of tan square x. Now it will be tan x whole square upon d tan x into d tan x upon dx. After we apply the xn formula, it will be two tan x times sec squared x. So the derivative of tan square x is two tan x sec squared x.

Let, y = tan^2x

dy/dx = d/dx (tan^2x) = d(tanx)^2 /d(tanx) times d(tanx)/dx

Next, dy/dx= 2 tanx times sec^2x

Next = dy/dx = 2tan sec^2x.

Derivative of log (sec x + tan x)

We have a derivative of the log of sec x plus tan x. So, let y be equal to the log of sec x plus tan x. Differentiate with respect to x, dy upon dx equal to the derivative of log sec x plus tan x. We can’t use the direct formula of log in this equation. So, we use log sec x plus tan x upon sec x plus tan x into the derivative of sec x plus tan x upon dx. However, log x is equal to 1, and log sec x plus tan x equals sec x times tan x plus sec squared x. Then we common the sec x, and it will be (sec x+ tan x) upon (sec x+ tan x). Next, both (sec x+ tan x) are canceled. At last, the derivative of log sec x plus tan x is equal to sec x.

Let y = (log (sec x + tan x))

Differentiate w.r.t.x

dy/dx= 1/(sec x + tan x) × d/dx (sec x + tan x)

Next, dy/dx = [1/(sec x + tan x) ]× sec x tan x + sec2x

= [1/(sec x + tan x)] × sec x (tan x + sec x)

= sec x

Derivative of y=tan x -1/ sec x

We have a derivative of y equals tan x minus one upon sec x. So, y dash can be equal to the tangent of an x minus one prime secant of x minus tan x minus one time the secant of x prime. Next, we get the derivative of the tangent, which is secant squared x and times secant of x, minus (tangent of x minus 1) times sec x tan x. Then we will get sec cube x minus tan squared x sec x plus sec x tan x. After some calculation, we have an identity which is sec squared x minus tan squared x plus tan x upon sec x. At last, the derivative of tan x -1/ sec x is one plus tan x upon sec x. Read Also:Derivative of Sin2x | Formula, Proof, Rules & Examples

Y dash = (tanx-1)dash sec x – (tanx-1) sec x dash = sec^2x · sec x- (tanx-1)sec x tan x

Y dash = sec^3x – tan^2x sec x + secx tanx

Next, y dash = sec^2x-tan^2x +tanx/sec x = 1 +tan x/sec x

Derivative of tan x^ cot x

• Let y equals tan x to the power cot x. The first method, a to the power b equals to e to the power b log a. So, y equals to e to the power cot x log tan x. Differentiate with respect to x, dy upon dx equals to e to the power cot x log tan x into differentiate cot x into log tan x. Now, We will use the product rule. Then we get tan x to the power cot x times cot x into the differentiation of log tan x plus log tan x into the differentiation of cot x.
• Now, it equals tan x to the power cot x into cot x times 1/tan x into sec square x plus log tan x into minus cos square x. Next, it will be tan x to the power cot x, and in the third brackets, cos x/sinx into cos x/sin x into 1/cos^2x minus log tan x into cosec^2x. Now we are canceling the cos x. Then dy/dx equals tan x to the power cot x into cosec square x minus cosec square x into log tan x. After some calculation, the answer is tan to the power cot x into cosec^2x into one minus log tan x.

Let, y=tanx^cot(x)

Then, log y = log tan(x)^cot(x)

Then, log y= cot(x).log(tanx).

Next, 1/y.dy/dx=cotx.(1/tanx).sec^2x-cosec^2x.log tanx.

Next, 1/y.dy/dx=cosec^2x-cosec^2x.log tan x

Now, dy/dx=y.cosec^2x(1-log tanx)

Now, dy/dx=tanx^cotx.cosec^2x.(1-log tan x)

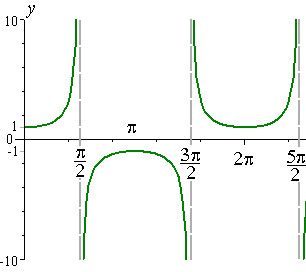
Graph of sec x

At first, the numbers are going to intersect at 1 minus 1 and back up at 1 again. Next we have asymptotes and 90 degrees, 270 degrees, because we cant have 1 over 0. Then the graph is going to fit around doing the opposite of decimal. So, 1 over this decimal between 0 and 90 is gonna show us a big value. 1 over the negative decimals between 90 and 270 are going to give us bigger negative values. Next 1 over values of the decimal were between 270 and 360 are gonna give us big values. However, intersection points at 0 degrees, 360 degrees and 180 degrees are undefined whenever the graph is equal to zero.

Integral of sec x dx

• If we write the secant of x as one over the cosine of x which is its definition, we try to integrate; unfortunately this expression here is not integratable. However we are going to have to manipulate this integrand to get into a form that we can integrate. Now there are probably a multitude of ways we can do this. But we can do this with two common ones. First one is to use partial fractions. Now in this first method, it will take quite a few steps and it is a robust method. Because in the second method, it requires a bit more intuition and it requires converting this integral into the form of f prime x over f of x. Then the result is going to be the log of the function. So, basically the second method uses a u substitution.
• So, in the partial fractions, we have established sec x that can be written as 1 over the cos of x. Now, this is equivalent if we multiply the top and bottom of this fraction by cos of x. So, we are multiplying by 1, the top becomes cos of x and the bottom becomes cos squared of x. Next, we can rewrite this because the identity (cosine squared x + sine squared x) is equal to 1. Then we can rewrite the bottom or the denominator as (1 – sine squared x).
• Next we can rewrite the sec x as sec x multiplied by sec x plus tan x divided by sec x plus tan x. Then we need to multiply this by one and we expand sec x into the numerator. However, we get sec squared x plus sec x tan x over the denominator (sec x+ tan x). Now, the integral of sec x is completed.

Formula of Sec x

The formula of secant of x is 1 divided by the cosine of x: sec x = 1 cos x.

Some frequently asked questions

What is the derivative of tan sec x?

Sec 2x is the derivative of tan sec x.

Is SEC 2x always positive?

Yes, sec 2x is always positive.

What is tan 2x equal to?

Sin 2x/cos 2x is equal to tan 2x.

Is tan 2x 1 Sec x a Pythagorean identity?

Yes, tan 2x 1sec x is a Pythagorean identity.

What is the relation between Tan X and Sec x?

The relation between tan x and sec x are tan x = sin x cos x.

What is tan 1x?

tan−1x = tan−1(x).

What is the derivative of SEC 2x?

f'(x) = 2 secx d/dx(sec x) = 2 sec x (sec x tan x) = 2 sec2x tan x is the derivative of sec 2x.