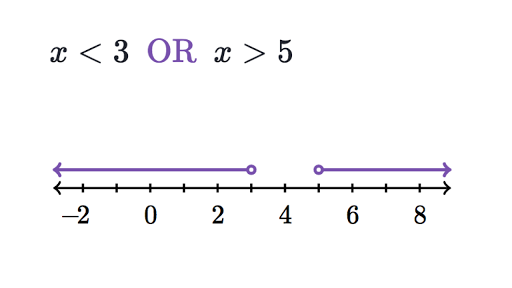Compound Inequality calculator: Definition, Examples, Graphs and more

When a compound inequality is specified, the Compound Inequality Calculator presents the inequality equation with a number line representation. Any online compound inequality calculator tool will speed up the computation and display the inequality equation in a matter of seconds.

The inequality calculator calculates the value of the variable based on the specified inequality. Inequality is a connection that is formed by comparing two integers or algebraic expressions. Inequalities, unlike equations, do not have equal mathematical expressions.

In this article, we are talking about this calculator. So, please keep reading to know more about it.

Compound Inequality calculator definition

The Inequality Calculator is an online application that assists in calculating the values of the variables in a particular inequality. In an inequality, the two statements are linked by the “greater than,” “less than,” or “not equal to” marks. Enter values into the input fields to utilise this inequality calculator.

Compound Inequalities is a method for determining the variable value of a set of compound inequalities. The words ‘and’ or ‘or’ would connect the two disparities. It is given in the form of a number line. When the arrows on the number line point in opposite directions, the inequalities are united by ‘and’; when the arrows point in the same direction, the inequalities are joined by ‘or’. Enter the Compound Inequalities into this Compound Inequality calculator to discover the variable value.

Compound Inequality calculator with steps

First Step: Navigate to the online inequality calculator at Cuemath.

Second Step: Enter the inequality into the inequality calculator’s input fields.

Third Step: Click the “Solve” button to compute the variable value for the provided inequality.

Fourth Step: Select “Reset” to clear the fields and input new values.

Compound Inequality calculator interval notation

The collection of real numbers that fall between any two given real numbers. It was expressed via interval notation. Inequalities can be represented by intervals. There are four types of intervals. If we have two endpoints, x and y, and x y, we may categorise the intervals as follows:

Intervals Are Open

This does not include the two ends. If we have a number z that is between x and y, we may write the inequality as x z y. Round brackets represent an open interval, i.e. (x, y).

Closed Intervals

This range includes both ends. The inequality is represented as x z y. Square brackets are used to denote closed intervals, such as [x, y].

Interval to the Right Half-Closed

In this interval, just the left endpoint is included, while the right endpoint is excluded. The inequality is denoted by x z y. The interval’s left side is contained by a square bracket, while its right side is enclosed by a round bracket, i.e., [x, y].

Only the right endpoint is included in this interval, whereas the left is excluded. The inequality is x z y. The left side utilises a circular bracket, but the right side uses a square bracket, i.e. (x, y).

The following formula may be used to calculate the length of the distance between x and y:

Length equals y minus x.

Inequality	Interval
x less than 2	(-∞, 2)
x greater than 2	(2, ∞)
x less than equals 2	(-∞, 2]
x greater than equals 2	[2, ∞)
two less than x less than equals 6	(2, 6]

Example 1

A person must be at least 35 years old to be elected President of the United States. Give an interval to represent this data.

Solution:

Let’s use A to symbolise the president’s age.

A’s age should be at least 35.

This indicates that A must be bigger than or equal to 35.

As a result, the inequality, A greater than equal 35, represents this.

As a result, the needed interval is [35, infinity].

A school’s participation in an Olympiad exam requires a minimum of ten pupils. Use interval notation to represent this.

Solution:

If x represents the number of pupils in a class, x should be larger than or equal to 10.

This translates to x greater than equal10

[10,infinity] is the interval notation.

As a result, [10,infinity] represents the number of pupils.

Lola needs at least 1500 calories per day, but her calorie intake should not surpass 1800. Using interval notation, represent the total number of calories she might consume.

Solution:

Let’s double the quantity of calories by x.

1500 inequality x inequality 1800 gives the inequality expressing the potential number of calories.

The interval notation [1500, 1800] denoted the inequality.

[1500, 1800] is the needed interval notation.

Compound inequality calculator graph

A compound inequality consists of at least two inequalities. So, “and” or “or” separated it. The graph of a compound inequality with a “and” represents the intersection of the graphs of the inequalities. If a number is a solution to both inequalities, it is a solution to the compound inequality. It represents x greater than -1 and x less than 2 or x -1 less than x less than 2. The graph of a compound inequality with a “or” reflects the union of the inequalities’ graphs. If a number is a solution to at least one of the inequalities, it is a solution to the compound inequality. So, x less than -1 or x greater than 2 denoted it.

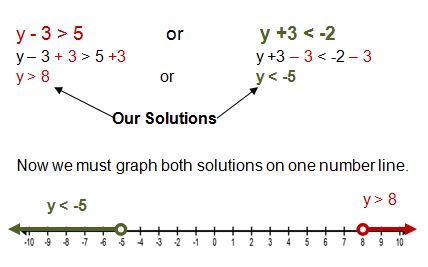
Points

We must keep the following points in mind when graphing inequalities.

Use a closed circle if the endpoint is included (i.e., in the case of or).
Use an open circle if the endpoint is NOT included (i.e., in the case of or greater than).
Then, use an open circle at + or -.
If the variable is more than the number, draw a line from the endpoint to the right side.
If the variable is less than the number, draw a line from the endpoint to the left.

To graph inequalities with two variables, first draw the “equals” line and then colour the relevant region. There are three steps to take:

Make the equation in such a way that “y” is on the left and everything else is on the right.

Draw the “y=” line (a solid line for y less than equals or y greater than equals, and a dashed line for y less than or y greater than).

Shade the region above the line if the value is “more than” (y greater than or y greater than equal) or below the line if the value is “less than” (y less than or y less than equal).

Let us look at an example: The following is a graph showing a linear inequality: y less than equals x + 4.

The y = x + 4 line may be seen, and the shaded region indicates where y is less than or equal to x + 4.

Compound inequality calculator with number line

To graph compound inequalities on a number line, you must do the following:

Solve the inequalities, i.e., convert them to, say, x greater than equals a.
Determine the value based on the first inequality on the number line.
Draw a line from that point to the: Left for less than and, or Right for greater than.
Draw the line up as follows: Slanted for strict inequalities (i.e., less than and greater than); or Straight for non-strict inequalities (i.e., less than equal and greater than equal).
Rep points 2-4 with various colours for consecutive disparities.
Find the point where all of the colours come together.
This region denotes the solution set for your compound inequalities.

Compound inequality calculator with or

To solve a compound inequality, divide it into two inequalities first. Determine if the response should be a set union (“or”) or a set intersection (“and”) (“and”). Then, solve both inequalities and graph the results.

Example 1

Solve and graph: 4 less than equal 2x less than equal 8

4 less than equal 2x and 2x less than equal 8 (intersection of sets)

4 less than equal 2x,

4/2 less than equals 2x/2

2 less than equal x

x greater than equal 2

2x less than equal 8

2x/2 less than equal 82

x less than equal 4

2 less than equal x and x less than equal 4.

Example 2

Solve and graph: {x : 5 less than equal x/3 +5 less than 6}

5 less than equal x/3 + 5 and x/3 +5 less than 6 (intersection of sets)

5 less than equal x/3 + 5

0 less than equal x/3

0 less than equal x

x/3 +5 less than 6

x/3 less than 1

0less than equal x and x less than 3.

Example 3

Solve and graph: 3(x – 2) less than 9 or 3(x – 2) greater than 15 (union of sets)

3(x – 2) less than 9

x – 2 less than 3

x less than 5

3(x – 2) greater than 15

x – 2 greater than 5

Then, x greater than 7

x less than 5 or x greater than 7.

Example 4

Solve and graph: {x : 2x less than equal x – 3} ∪ {x : x less than 3x – 4}

2x less than equal x – 3 or x less than 3x – 4 (union of sets)

2x less than equal x – 3

x less than equal – 3

x less than 3x – 4

-2x less than – 4

x greater than2

x less than equal – 3 or x greater than 2.

Example 5

Solve and graph: 2x – 2 less than – 2 or 3(x + 5) greater than 2x + 15 (union of sets)

2x – 2 less than – 2

2x less than 0

x less than 0

3(x + 5) greater than 2x + 15

3x + 15 greater than 2x + 15

3x greater than 2x

x greater than 0

x less than 0 or x greater than 0.

Compound inequality calculator example

Compound inequalities are a group of inequalities that have either “and” or “or” in between them. In this situation, to solve inequalities, just solve each inequality individually and then obtain the final answer using the following rules:

If there is a “and” between the solutions, the final solution is the intersection of the solutions of the independent inequalities.
If there is a “or” between the solutions, the final solution is the union of the solutions of the independent inequalities.

Solve the compound inequality 2x + 3 less than -5 and x + 6 less than 3.

Solution:

By first inequality:

2x + 3 less than -5

2x less than -8

x less than -4

By second inequality,

x + 6 less than 3

x less than -3

Because there is a “and” between them, we must locate the intersection of the sets x less than -4 and x less than -3. In this scenario, a number line may be useful. The final solution is as follows: x less than -3 (or) (-∞, -3).

Compound inequality calculator uses

The steps for resolving disparities are as follows:

Convert the inequality into an equation.
Find the solution to the equation for one or more numbers.
Draw a number line to represent all of the values.
Use open circles to indicate all omitted values on the number line.
Determine the intervals.
Choose a random number from each interval, enter it into the inequality, and see if the inequality is satisfied.
Satisfied intervals are the solutions.

However, algebraic operations like addition, subtraction, multiplication, and division are commonly used to solve basic inequalities (linear). Consider the following scenario:

2x + 3 greater than 3x + 4

Subtracting 3x and 3 from both sides,

2x – 3x greater than 4 – 3

-x greater than 1

Multiplying both sides by -1,

x less than -1

We have increased inequality by a negative value on both sides. The above-mentioned approach for solving inequalities works for a basic linear inequality. To solve any other complicated inequality, however, we must apply the following procedure.

Compound inequality calculator

A compound inequality is a phrase that has two inequality claims connected by the words “or” or “and.” The conjunction “and” denotes that both statements of the compound phrase are true at the same time. It is the intersection or overlap of the solution sets for the particular assertions. The word “or” signifies that the entire compound phrase is true if either assertion is true. It is the union or combination of the solution sets for the individual assertions. A conjunction is a compound inequality that contains the word “and.” Although “and” and “or” are both conjunctions, the mathematical conjunction has a distinct meaning than the grammatical conjunction.

3 x + 2 less than 14 and 2 x – 5 greater than –11 are the solutions for x.

Separately solve each inequality. Because the linking word is “and,” it implies that the overlap or intersection is the desired outcome.

x less than 4 represents all of the numbers to the left of 4, while x greater than –3 represents all of the numbers to the right of –3. All the integers between –3 and 4 are found at the intersection of these two graphs.

The solution set consists of { x| x greater than –3 and x less than 4}

Another method to represent this solution set is { x|–3 less than x less than 4}

When a compound inequality is written without the words “and” or “or,” it is assumed to be the word “and.” Reading x|–3 x 4 from the ” x” position, you argue (to the left) that x is larger than –3 and (to the right) that x is less than 4. Figure 1 depicts the solution set’s graph.

Figure 1 shows that x is larger than –3 but less than 4.

Compound Inequality calculator linear

A linear inequality is one that may be represented using a linear expression on one side and a 0 on the other. Solving linear inequalities is the same as solving linear equations, except only the rules for solving inequalities (as previously mentioned) must be followed. Let us look at a few examples.

Take a look at the inequality 2x less than 6. To solve this, only one step is required: divide both sides by 2. Then we have x less than 3. As a result, the solution to the inequality is x less than 3 (or) (infinity-, 3).

Consider the following inequality: -2x + 3 greater than 6. We need to take two actions to remedy this. The first step is to remove 3 from both sides, yielding -2x greater than 3. Then we divide both sides by -2, which yields x less than -3/2. (note that we have changed the sign of the inequality). As a result, the solution to the inequality is x less than-3/2 (or) (-infinity, -3/2).

Compound Inequality calculator values

In an absolute value inequality, an algebraic expression is enclosed by the absolute value sign. Here is the procedure for solving absolute value inequalities, with an example of solving an absolute value inequality |x + 3| 2.

Think of the absolute value inequality as an equation.

|x + 3| equals 2

Work out the equation.

x + 3 = 2

Then, x + 3 = -2

Then, x + 3 = -1; x = -5

On the number line, represent the numbers from Step 2 and indicate the intervals.

Because less than equal contains “=”, we use closed brackets at -1 and -5.

Select a random integer from each of the aforementioned intervals for testing and see if the provided inequality is fulfilled.

The solution intervals are the intervals that satisfy the inequality.

As a result, the answer to the absolute value inequality |x + 3| less than equal 2 is [-5, -1].

Some frequently asked questions

How do you find the compound inequality?

Compound Inequalities is a method for determining the variable value of a set of compound inequalities. The words ‘and’ or ‘or’ would connect the two disparities. When the arrows on the number line point in opposite directions, ‘and’ unite the inequalities; when the arrows point in the same direction, ‘or’ join the inequalities. Enter the Compound Inequalities into this Compound Inequality calculator to discover the variable value.

What is a compound inequality example?

Solve the compound inequality 2x + 3 less than -5 and x + 6 less than 3.

Solution:

By first inequality:

2x + 3 less than -5

2x less than -8

x less than -4

By second inequality,

x + 6 less than 3

x less than -3

What is compound inequality in math?

A compound inequality is one that is formed by combining two simple inequalities.

Can you subtract inequalities?

Our aim while solving inequalities by subtraction is to have the variable on its own. It might occur on either the bigger or smaller side of the inequality. Subtracting a number from both sides of the inequality has no effect on the inequality’s direction.

Pages

Categories

Compound Inequality calculator: Definition, Examples, Graphs and more

Compound Inequality calculator definition

Compound Inequality calculator with steps