Before we go into the concept of a horizontal asymptote, let’s define a function. A function is an equation that shows how two things are related. Typically, functions explain how y is connected to x. Functions are frequently graphed to offer a visual representation. A horizontal asymptote is a horizontal line that indicates how a function will behave at the graph’s extreme edges. A horizontal asymptote, on the other hand, is not hallowed ground. The function can get close to, and even cross, the asymptote. Horizontal asymptotes occur for functions with polynomial numerators and denominators. These are known as rational expressions.

A function’s horizontal asymptote is a horizontal line with which the function’s graph looks to coincide but does not truly coincide. The horizontal asymptote identifies the function’s final behaviour. In this article, we are talking about this asymptote. So, please keep reading to know more about it.

Horizontal Asymptotes definition

When either lim x f(x) = k or lim x – f(x) = k, the horizontal asymptote of a function y = f(x) is a line y = k. That is, it is a line that the function’s graph (curve) seems to approach as x or x -. It is commonly abbreviated as HA. In this case, k is a real number that the function approaches when the value of x is either extraordinarily big or extremely tiny. A horizontal asymptote may or may not exist for a function. However, the greatest number of asymptotes a function may have is two. In other words, a function can contain 0 asymptotes, 1 asymptotes, or 2 asymptotes.

A dotted horizontal line is commonly used to indicate a horizontal line. When the x-axis is the HA, we don’t normally use the dotted line to represent it.

Read Also: Difference Quotient – Meaning, Formula, Calculation, Derivation

It is worth noting that we find the HA while charting a curve just to indicate the value that the function is approaching. However, because it is not a component of the curve, it is not required to depict it while graphing it. Even graphing calculators fail to display a horizontal line for the horizontal asymptote. A horizontal line, in other terms, is a fictitious line.

Horizontal Asymptotes finder

While vertical asymptotes explain a graph’s behaviour as the output becomes extremely big or very tiny, horizontal asymptotes help describe a graph’s behaviour when the input becomes very large or very small. Remember that the end behaviour of a polynomial will be the same as the leading term. Similarly, the end behaviour of a rational function will be the same as the ratio of the leading terms of the numerator and denominator functions.

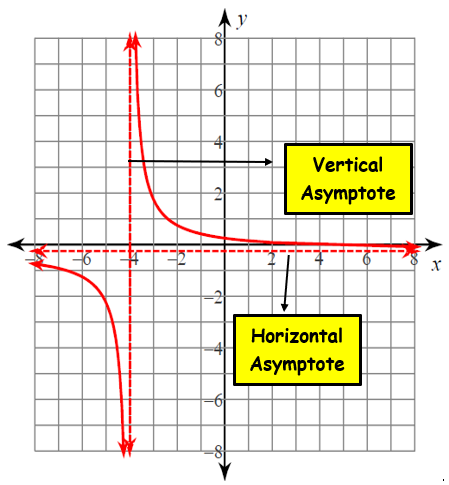
When looking for horizontal asymptotes, there are three possible outcomes:

Example 1

There is a horizontal asymptote at y = 0 if the degree of the denominator is greater than the degree of the numerator.

f(x) = 4x + 2/ x^2 + 4x – 5

In this situation, the final behaviour is f(x) approximately equal to 4x/x^2 =4/x.

A formalised paraphrase This means that when the inputs rise or decrease without bound, this function will behave similarly to g(x) = 4/x, and the outputs will approach zero, giving rise to a horizontal asymptote at y = 0. It is worth noting that this graph passes the horizontal asymptote.

Example 2

A slant asymptote is obtained by multiplying the degree of the denominator by the degree of the numerator.

f(x) = 3x^2 – 2x +1/ x-1

In this situation, the desired outcome is f(x) approximately equal to 3x^2/x = 3x. This means that if the inputs are not constrained, this function will operate similarly to the function g(x) = 3x. As the inputs increase in size, the outputs increase and do not level out, hence this graph lacks a horizontal asymptote. However, the graph of g(x) = 3x seems to be a diagonal line y = 3x, and because f behaves similarly to g, it will approach a line near to displaystyle y=3xy=3x. This is a slant asymptote line.

Divide 3x^2 – 2x +1/ x-1 to determine the equation of the slant asymptote. 3x+1 is the quotient, and the remainder is 2. The graph of the line is the slant asymptote g(x) = 3x + 1.

Example 3

If the degree of the denominator equals the degree of the numerator, a horizontal asymptote exists at y = a n/ b n, where a n and b n are the leading coefficients of p(x) and q(x) for f(x)= p(x)/ q(x), q(x) not equal 0.

f(x) = 3x^2 + 2/ x^2 + 4x – 5

In this example, the final behaviour is f(x) approximately equal to 3x^2/x^2 = 3. This indicates that when the inputs increase in size, this function will behave similarly to the function g(x)=3, which is a horizontal line. As x tends to plus minus infinity, a horizontal asymptote at y = 3 is obtained. It is worth noting that this graph passes the horizontal asymptote.

A rational function’s graph will never cross a vertical asymptote, but it may or may not cross a horizontal or slant asymptote. In addition, whereas the graph of a rational function may have multiple vertical asymptotes, it will only have one horizontal (or slant) asymptote.

It should be noted that if the degree of the numerator is greater than one greater than the degree of the denominator, the graph’s end behaviour will mirror the behaviour of the decreased end behaviour fraction. For example, if we had the function

f(x) = 3x^5 – x^2/ x+ 3

f(x) approximately equal to 3x^5/ x = 3x^4

The graph’s final behaviour would be comparable to that of an even polynomial with a positive leading coefficient.

X tends to plus minus infinity, f(x) tends to infinity.

Horizontal Asymptotes how to find

Horizontal asymptotes are horizontal lines that the function graph approaches as x tends to plus minus infinity. If the horizontal line y = c is a horizontal asymptote of the function y = (x), it is a horizontal asymptote of the function y = (x).

Limit at x tends to minus infinity f(x) equals c or Limit at x tends to plus infinity f(x) equals c.

In the first example, f(x) has y = c as an asymptote when x tends to infinity, whereas in the second case, f(x) has y = c as an asymptote when x goes to + infinity.

The arctangent function, for example, satisfies:

Limit at x tends to infinity arctan(x) equals minus pi/2 and Limit at x tends to plus infinity arctan(x) equals pi/2.

So when x tends to – infinity, the line y = −pi/2 is a horizontal asymptote for the arctangent, and when x tends to + infinity, the line y = /2 is a horizontal asymptote for the arctangent.

Functions may be devoid of horizontal asymptotes on one or both sides, or they may have a single horizontal asymptote that is the same in both directions. For example, when x goes to and +, the function (x) = 1/(x2+1) exhibits a horizontal asymptote at y = 0 because

Limit at x tends to infinity 1/x^2 plus 1 equals Limit at x tends to plus infinity 1/x^2 plus 1 equals 0.

Horizontal Asymptotes of Rational function

A rational function can only have one horizontal asymptote. Though we may use the limits to get the HAs, the following approaches provide an easier way to locate the horizontal asymptotes of rational functions:

• If the degree of the numerator is greater than the degree of the denominator, the function has no HA.
• Then, if the degree of the denominator is greater than the degree of the numerator, the function has one HA, which is y = 0.
• If the numerator’s degree equals the denominator’s degree, the function has one HA, which is y = the ratio of the numerator and denominator’s leading coefficients.

In the preceding section’s example (where f(x) = 2x / (x – 3)), the degree of the numerator equals the degree of the denominator (= 1). As a result, the HA of f(x) is y = 2/1 = 2. It’s worth noting that we obtained the same response even when we applied the limitations. Here are a few more instances.

• y = (x2+3) / (2x) has no HA.
• HA of y = (2x) / (x2 + 3) is y = 0.
• HA of y = (2×2) / (x2 + 3) is y = 2.

Example 1

Determine each rational function’s horizontal asymptote:

f(x) = 4x^2 – 5x/ x^2 – 2x +1

The degrees of the polynomials must first be compared. Both the numerator and denominator are polynomials of the second degree. Because they are of the same degree, the coefficients of the highest terms must be divided.

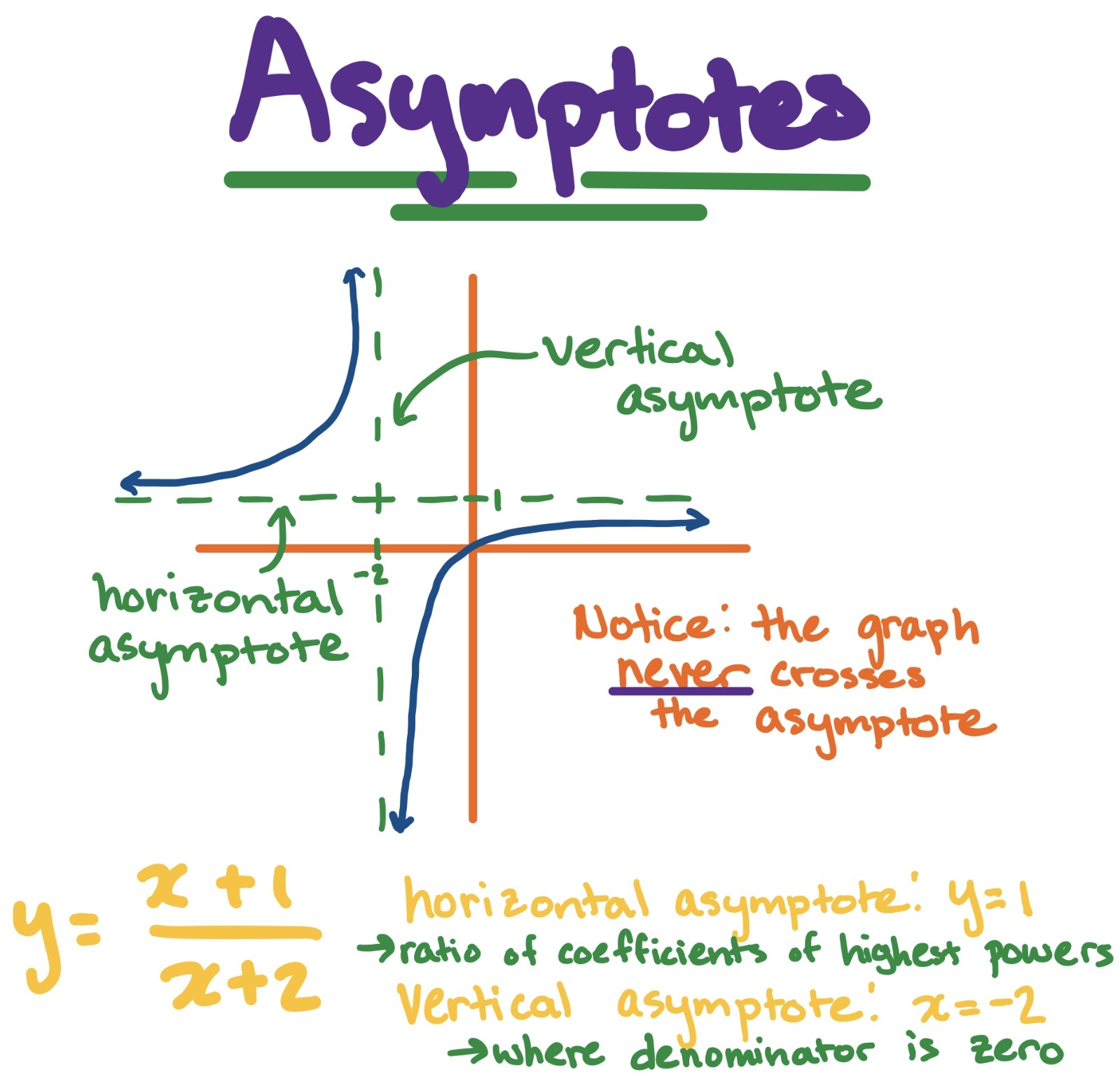
The coefficient of the highest term in the numerator is 4.

The coefficient of the highest term in the denominator is a known 1.

4/1 = 4

At y = 4, the horizontal asymptote is reached.

Example 2

f(x) = x^2 – 9/ x+ 10

The degrees of the polynomials must first be compared. The numerator includes a polynomial of second degree, whereas the denominator contains a polynomial of first degree.

There is no horizontal asymptote because the polynomial in the numerator has a greater degree than the denominator. Instead, there is a slant asymptote.

Example 3

f(x) = x – 12/ 2x^3 + 5x – 3

The degrees of the polynomials must first be compared. A first degree polynomial is in the numerator, while a third degree polynomial is in the denominator.

Because the polynomial in the numerator has a lower degree than the polynomial in the denominator, the horizontal asymptote is at y=0.

Horizontal Asymptotes calculator

Asymptote Calculator is a free online calculator that displays the asymptotic curve for a given equation. The online asymptote calculator tool on any website speeds up the calculation and shows the asymptotic curve in a matter of seconds.

The following is how to use the asymptote calculator:

• First, type the expression into the input box.
• Then, to obtain the curve, click the “Submit” button.
• Finally, in the new window, the asymptotic curve will be presented.

The asymptote is defined in mathematics as a horizontal, vertical, or slanted line that the graph approaches but never touches. In analytic geometry, the asymptote of a curve is a line whose distance from the curve approaches zero. The indicated circumstance occurs when one or both coordinates (x and y coordinates) trend to infinity. There are three types of asymptotes: horizontal asymptotes, vertical asymptotes, and oblique asymptotes.

Horizontal Asymptotes rules

Let us review all of the horizontal asymptote laws we’ve encountered thus far.

Get the degrees of the numerator (n) and denominator (d) of a rational function to find its horizontal asymptote (d).

• If n less than d, then HA equals y = 0.
• Then, if n exceeds d, there is no HA.
• If n = d, then HA is y = leading coefficient ratio.
• y = c is the horizontal asymptote of an exponential function of the type f(x) = abkx + c.

A polynomial function (such as f(x) = x+3, f(x) = x2-2x+3, and so on) cannot have a horizontal asymptote since the limits of these functions as x trend to or – do not yield real integers.

To identify the horizontal asymptote of any other function except these, we just use the standard approach of applying limits as x tends to infinity and x – infinity.

Horizontal Asymptotes formula

Another method for determining a rational function’s horizontal asymptote is to divide N(x) by D. (x). If the quotient is constant, the equation of a horizontal asymptote is y = this constant.

Horizontal Asymptotes equation

We know that the vertical asymptote for the graph function y = f(x) has a straight line equation is x = an if it meets at least one of the following conditions:

Limit of x tends to a – 0 f(x) = plus minus infinity

or

Limit of x tends to a + 0 f(x) = plus minus infinity

Otherwise, one of the one-sided limits at x=a must be equal to infinity.

The limit of the oblique asymptote of the graph function y=f(x) for the straight-line equation is y=kx+b.

X tends to plus infinity

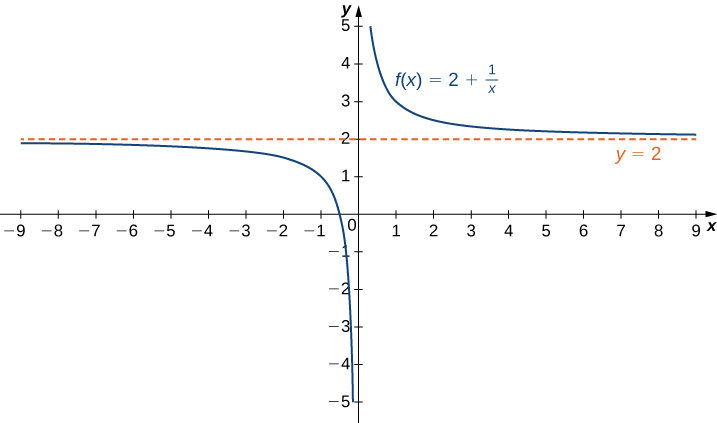
If and only if the following two constraints are met.

Limit of x tends to plus infinity f(x)/x = k.

Limit of x tends to plus infinity [f(x) – kx] = b.

For the graph function y=f(x) where, the straight line equation is y=b, which is the asymptote of a function.

X tends to plus infinity, assuming that the following limit is finite.

Limit of x tends to plus infinity f(x) = b.

The aforementioned limit applies to both

x tends to minus infinity.

Example

Determine the asymptotes for the function f(x) = (3x – 2)/(x + 1)

Solution:

Given,

(3x – 2)/(x + 1) Equals f(x).

For x = -1, f(x) is not defined.

Find the one-sided bounds of the following function when x = -1.

Limit x tends to – a – 0 f(x) = limit x tends to minus 1 minus 0 3x – 2/ x + 1= -5/-0 = + infinity.

Limit x tends to – a + 0 f(x) = limit x tends to minus 1 plus 0 3x – 2/ x + 1= -5/0 = – infinity.

As a result, when x = -1, the function f(x) possesses a vertical asymptote.

Let us now determine the horizontal asymptotes by taking x tends to plus minus infinity.

Limit of x tends to infinity f(x) = limit of x tends to infinity 3x – 2/ x + 1 = Limit of x tends to infinity (3 – 2/x) / 1+1/x = 3/1 = 3

As a result, when y = 3, the function f(x) possesses a horizontal asymptote.

K = limit of x tends to infinity f(x)/ x

= limit of x tends to infinity 3x – 2/ x( x+1)

= limit of x tends to infinity 3x-2/ (x^2 + x)

Then, =0/1 = 0

Likewise, we may get the same number for x – infinity.

There are no oblique asymptotes for the given function since k = 0.

Horizontal Asymptotes examples

Example 1

Find the horizontal asymptote of y = (3×2+2x)/(x+1).

Solution:

The degree of the numerator in this case is 2.

The denominator’s degree Equals 1.

As a result, the degree of the numerator is greater than the degree of the denominator.

As a result, f(x) has no HA.

Answer: There is no HA in the supplied function.

Example 2

Determine the value of k using the horizontal asymptote rules if the HA of f(x) = 2x – k equals y = 3.

Solution:

We know that the vertical transformation of an exponential function determines its HA.

As a result, the HA of f(x) = 2x – k is y = -k.

However, it is assumed that the HA of f(x) equals y = 3.

As a result, -k = 3 (or) k = -3.

k = -3 is the answer.

Example 3

Determine the horizontal asymptotes of f(x) = x/x2+3.

Solution:

Given that f(x) = x/x2+3,

Because the degree of the numerator is smaller than the degree of the denominator, the horizontal asymptote is placed at y = 0.

Example 4

Determine the horizontal asymptotes of f(x) =(x2+3)/x+1.

Solution:

Given that f(x) = (x2+3)/x+1

As you can see, the numerator has a higher degree than the denominator. As a result, there is no horizontal asymptote.

Some frequently asked questions

How do you find the horizontal asymptote?

Horizontal asymptotes are horizontal lines that the function graph approaches as x tends to plus minus infinity. If the horizontal line y = c is a horizontal asymptote of the function y = (x), it is a horizontal asymptote of the function y = (x).

The arctangent function, for example, satisfies:

Limit at x tends to infinity arctan(x) equals minus pi/2 and Limit at x tends to plus infinity arctan(x) equals pi/2.

So when x tends to – infinity, the line y = −pi/2 is a horizontal asymptote for the arctangent, and when x tends to + infinity, the line y = /2 is a horizontal asymptote for the arctangent.

What is its horizontal asymptote?

A function’s horizontal asymptote is a horizontal line with which the function’s graph looks to coincide but does not truly coincide. The horizontal asymptote identifies the function’s final behaviour. In this article, we are talking about this asymptote.

What are the 3 different cases for finding the horizontal asymptote?

• There is a horizontal asymptote at y = 0 if the degree of the denominator is greater than the degree of the numerator.
• A slant asymptote is obtained by multiplying the degree of the denominator by the degree of the numerator.
• If the degree of the denominator equals the degree of the numerator, a horizontal asymptote exists at y = a n/ b n, where a n and b n are the leading coefficients of p(x) and q(x) for f(x)= p(x)/ q(x), q(x) not equal 0.

What is the vertical asymptote?

A vertical asymptote is a vertical line that directs the function graph but is not a part of it. It can never be crossed by the graph since it happens at an x-value that is outside of the function’s scope. There may be more than one vertical asymptote for a function.

How do you identify vertical and horizontal asymptotes?

Apply the limit x tends to infinity or x tends to – infinity to locate the horizontal asymptotes. Apply the limit y tends to infinity or y tends to -infinity to determine the vertical asymptotes. Divide the numerator by the denominator to determine the slant asymptote (if any).

What are the different kinds of asymptote?

Asymptotes are classified into three types: vertical, horizontal, and oblique. That is, when the function approaches infinity from either the positive or negative side, it approaches positive or negative infinity.

Are vertical asymptotes in the numerator or denominator?

These vertical asymptotes arise when the function’s denominator, n(x), is zero ( not the numerator). Near the values x = 1 and x = –1, the graph practically vertically ascends or descends, and the function tends to + infinity or − infinity.