So, calculus becomes an important part as soon as you go to high school. The utility of calculus is not limited just to your math syllabus. Therefore, be it physics, chemistry, economics, or statistics, you find the applications of calculus everywhere. So, when we begin with calculus, we first go through the first principle, limits, differentiation, or derivative, and then finally integration. Moreover, like the antiderivative calculator, there are calculators for all of these processes to help you out and make your job way easier. However, before that let us see what an antiderivative is and how it is linked with derivatives at large.

Therefore, we all know we find derivatives of a function with the process of differentiation. Now, the process of differentiation means breaking one entire function into infinitesimal small portions and then finding the value of each such portion. On the other hand, integration helps in finding integrals that join infinitesimal small parts of a function to find out the macro function. So, you can say that these two processes work against each other. Now, where does the antiderivative come in here? Hence, an antiderivative is a differentiable function F whose derivative is the same as the original function f. So, this is what the antiderivative calculator finds out. Moreover, you can also call this the inverse derivative, primitive function, primitive integral, or indefinite integral. Therefore, we write this symbolically as F’ = f
Hence, you do realize that when you are using an antiderivative calculator, you are using two functions some way or the other. So, you have the original function whose derivative you can find out. Moreover, you have to find another function whose derivative is the same as this function. Therefore, you realize that the function of the antiderivative calculator is integration.
General antiderivative calculator
So, it is already clear from the name what an antiderivative calculator does. Therefore, an antiderivative calculator does integrate the function that you feed into it. So, what comes before you is the final antiderivative or indefinite integral of the function. However, there can be various kinds of functions. As per the laws of integration, each integration needs a different sort of process. You can easily learn them as and when you do sums.
Therefore, when you choose an antiderivative calculator, choose wisely such that one calculator can support all your demands.

So, you need to remember that the process of finding antiderivatives or integrating is not as simple as differentiation or finding derivatives. The main reason behind this is that unlike in derivatives, you do not have the chain rule or the product or the quotient rule that allows you easy multiplication or division. Moreover, there is no way to find the integral of the function in a division form. So, you have to change it in some way. This is one of the hardest parts. As for the question of multiplication also, you have to apply a highly complex process. So, we call this integration by parts. However, we will not delve into these anymore.
Let us now shift our focus to which antiderivative calculator you must use amongst the prevailing ones.
Antiderivative calculator online
The internet makes everything very easy. Therefore, calculus is no different. So, calculus is one of the most difficult but important parts of math that you study in school. This is because this is going to be a very important foundation if you pursue any science course later on. So, a clear understanding of calculus is very important. Moreover, textbooks cannot always help you out with the best explanations. This is exactly why there are so many calculators that you can use online.
So, we have already seen what an antiderivative is and how we should find it out. However, our discussion has been largely theoretical. So, unless and until you see an example before you, understanding might not be easy. Therefore, this is what an antiderivative calculator does. When you use it, these complex-looking statements bear far more meaning and you gradually learn the process.
However, the basic part of an antiderivative calculator is to help you learn. So, do not use it just for your school homework, and copy down the answer blindly. Therefore, you should see the working of the antiderivative calculator and learn for yourself how to go about it.
Moreover, an antiderivative calculator that is available online has various benefits. We will see that in the next section of the article.
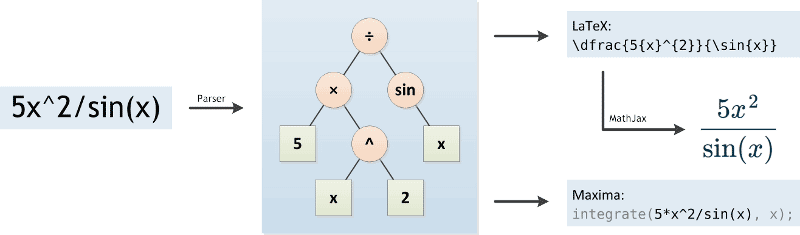
Antiderivative calculator Wolfram
In the world of calculators, Wolfram is an extremely popular name. So, Wolfram is like a warehouse of calculators that you can need for different mathematical functions. The range of tools that you have in Wolfram is highly impressive. So, the antiderivative calculator is one of the many calculators that Wolfram has and you can easily avail it. Moreover, the antiderivative calculator from Wolfram comes in the form of a widget. Therefore, this means that you can easily save it or implement it in your own document. So, you do not need to go online every single time you need the antiderivative calculator.
However, Wolfram Alpha does not give you the steps of the integration for free. No antiderivative calculator available online does that. Moreover, there are various other pages that use the widget from Wolfram Alpha. So, as soon as you want to see the steps, they will ask you for payment. However, the payment is a bare minimum. Hence, if you can afford it go for it because without the steps, using an antiderivative calculator is meaningless.
Now, as to why you should use an antiderivative calculator, the reasons are many. To begin with, we are human beings. So, making mistakes when working out manually is nothing big. However, in something as intricate as integrals, making a small error can cost you a lot by diverting the calculation. Therefore, you can simply use it to verify if you are on the right track. If you are a newbie, you would need to use the calculator to understand how it works till you can start doing it all by yourself. Moreover, it can be an effective device for tracking your mistakes and correcting them once you are done.
So, now let us check out an antiderivative calculator stepwise.
Antiderivative calculator with steps
So, in this case, we will be discussing the process stepwise with respect to the antiderivative calculator from Wolfram that we have already seen. The link to the calculator is given in the first step. Moreover, we will be taking an extremely simple function here for easier understanding.
Step 1 to use an antiderivative calculator
So, go to the Wolfram Alpha webpage first to get a hold of the calculator. Click on Wolfram Alpha and the link will directly take you to the page containing the antiderivative calculator. Therefore, on reaching the page, you find there is no specific small widget that you use as a calculator. So, there is a small horizontal bar at the top of the pages and a huge section at the bottom that reads “indefinite integrals”. Hence, this is the section where you get your solution after the operation is over.
Moreover, in the horizontal bar, there is a box in the shape of a search engine. Beside it, it reads “antiderivative of”. So, you have to enter the data that you want to compute.
Step 2 to use an antiderivative calculator
Therefore, now enter the function whose antiderivative or integral you want to find inside the box that looks like a search engine. Let us take a very simple function in the first case. Therefore, the function that we enter here is just x^2. After you have entered your function, either press the enter key or click on the solve button for the computation process to begin.
Step 3 to use an antiderivative calculator
So, the antiderivative calculator will take a couple of seconds as it runs your program. After this is over, you will be able to see the final solution in the section of indefinite integrals right below on the same page. So, in this case, the answer comes to be x^3/ 3 + constant. Therefore, remember that the presence of this constant is very important because it is an indefinite integral. It is impossible to find out definite integrals without any lower or upper limit.
So now, let us see how this happens. As per the power rules of integration, when you integrate any degree of the variable, the integral becomes one higher degree of x divided by the same degree. Therefore, the original question was x^2. You are integrating this with respect to x. So, making the degree high by one means x^3, and then dividing it by the same means x^3/ 3. Moreover, the constant is there as the integral is indefinite. Therefore, this is your final answer.
So, in simple terms, integration of x^y with respect to x is x^(y + 1)/ (y + 1). However, remember that y here is not another variable but just a numeric constant.
Step 4 to use an antiderivative calculator
Finally, there is an option in the solution box. It reads “Need a step-by-step solution for this problem?” in red. So, this is where you can get the steps from. However, this is an anchor link that will lead you to another page. Therefore, you can only see the full solution after you have subscribed to some package. However, the basic idea behind the antiderivative calculator remains the same as that of plain integration.
Antiderivative calculator with conditions
So, suppose your antiderivative calculator has to find out the specific antiderivative, let us say f(x) of a function let us say F(x). However, the initial condition is that f(a) = b. So, let us see how this works. To find this out, you need to follow some steps.
First, find out the general antiderivative of F(x) with its constant C.
So, after this, you place the initial conditions into the general antiderivative. Therefore, now you have to solve it to get the value of the constant C.
Hence now, place C into the general antiderivative formula. So, this will help you to find the specific antiderivative that you are looking for.
So, you realize that you conduct indefinite integration at the beginning. However, you have certain conditions with you that are additional information. So, you can use them to find out the value of the integration constant. Once you find this out, the antiderivative is no longer indefinite. You can place the value, and get the exact value of the antiderivative that you were looking for. This is crucial because in an antiderivative calculator you have no place to insert limits.
Antiderivative calculator using u substitution
So, this is nothing new when it comes to the process of integration. Therefore, we all use the substitution method when we need to find out some complex integrals. So, the basic idea behind this is that you substitute the function with u and then accordingly change the dx part. This makes the calculation way easier and smoother. So, after you have done it, you can simply put the original values of the substitution and you get your answer.
Read Also:Discriminant Calculator Online, Step by Step Explanation
Therefore, we use this a lot in the case of trigonometric functions where once you differentiate and substitute, you find the integral of another function from the process. The antiderivative calculator from Symbolab can help you out on this. Just click the link and it will take you directly to the calculator. Enter the value in the first box that looks like a search engine. Click the red button that reads “Go”.
Therefore, you will have the entire solution before you. However, calculus calculators are hardly free. So, if you want to gain access to the steps, you need to unlock them by getting yourself a subscription. However, knowing the steps are crucial for understanding the process.

Antiderivative calculator with bounds
So, an antiderivative calculator with bounds simply means that what you are finding out is a definite integral. Therefore, you have an upper limit as well as a lower limit. Your final antiderivative will lie in between these two bounds or limits. However, in most of the antiderivative calculators available online, you will not have the feature of inserting limits with the problem. However, that is nothing to worry about.
So, let the antiderivative calculator compute it as an indefinite integral. Therefore, you have the final answer along with the constant c. Now, it is a very simple calculation and you can manually put the limits. Just place the upper limit minus the lower limit in all the places the variable is placed. However, make sure to remove the constant because the integral is no more indefinite. And there you have your antiderivative with bounds.
Therefore, let us say, in the above example of integrating x^2, the upper limit was 3 and the lower 2.
So, your final answer would be (3^3/ 3) – (2^3/ 3). Therefore, this is equal to (27 / 3) – (8 / 3)
So, this gives 9 – (8 / 3). Therefore, the final answer is 19/3.
Antiderivative calculator FAQs.
What is the difference between an antiderivative and an integral?
Ans. Well, an antiderivative is essentially an indefinite integral. However, you cannot call a definite integral to be an antiderivative. So, the Venn diagram is such that all antiderivatives are integrals but the other way round is not true.
What does an antiderivative tell us?
Ans. So, an antiderivative simply reverses the function of the derivative. Therefore, it integrates infinitesimally small parts and gives us the macro value against a derivative that breaks up a macro value into infinitesimally small parts.
How do you find the antiderivative on a calculator?
Ans. Well, the process is extremely simple. You simply feed in the function whose antiderivative you want to find and run it. The antiderivative calculator does the rest for you.
What does c represent in an antiderivative?
Ans. Well, so the constant c is the exact same thing as that of the integration constant. So, you need it whenever you are doing an indefinite integral because of the fact that there are no limits.

What is antiderivative sin?
Ans. Well, the antiderivative of sin is simply its integral which as we all know is -cos. However, do not forget to include the integration constant c.
What is the symbol for antiderivative?
Ans. So, we generally write antiderivatives as F’ = f. However, to know what f or F’ means and how they are connected, scroll up and check the introductory part of the article. We have it covered in detail.
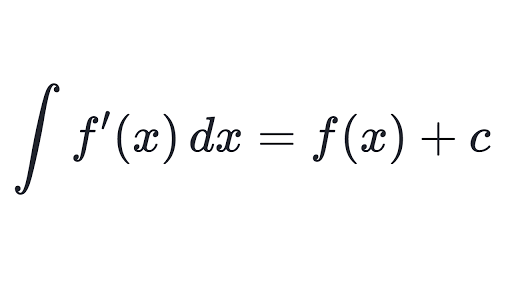
How many antiderivatives can a function have?
Ans. Well so, a continuous function can have an infinite number of antiderivatives. This is because we are using no limits here.
Who created antiderivatives?
Ans. So, in 1675, Gottfried Leibniz created the concept of integrals or antiderivatives for the first time.





