We refer to the angles with identical initial and terminal sides as coterminal angles. So, by adding or subtracting 360° or 2π to a given angle, we can find its coterminal angle. The functions of sin, cos, and tan have the same values for coterminal angles in trigonometry.

So, after you’ve grasped the concept, you’ll be able to distinguish between coterminal and reference angles, as well as solve issues using the coterminal angles formula.

Moreover, a coterminal angle calculator is a fun way to solve coterminal angle problems.

Coterminal angle calculator

We can calculate the positive and negative coterminal angles of a given angle stated in degrees by using the Coterminal Angle Calculator. We add or subtract 360 degrees from a coterminal angle to ascertain it. Enter the angle in the supplied input box to utilise the coterminal angle calculator.

A coterminal angle calculator is a fun way to solve coterminal angle problems.

How to use coterminal angle calculator

To use the coterminal angle calculator and to get the coterminal angles of a given angle, please follow the instructions below:

• Step 1: Use the online coterminal angles calculator at Cuemath.
• In the 2nd step: Enter the angle in the coterminal angles calculator’s input box.
• Step 3: To find the coterminal angles, click the “Calculate” button.
• Finally: To clear the fields and input new values, click the “Reset” option.

Thus, a coterminal angle calculator is a fun way to solve coterminal angle problems.

How does coterminal angle calculator work

Coterminal angles are angles that occupy the same place despite having different values. Their vertices are the same, and they are in the same quadrant on the same side. Thus, when a defined angle is turned clockwise or anti-clockwise and its terminal side coincides, a coterminal angle is generated.

Read Also: Combination Formula: Definition, Examples & more

Additionally, the initial side of the ray is known as the initial side, while the terminal side is known as the terminal side. When the difference between two angles is a multiple of 360 degrees, the two angles are said to be coterminal. Thus, to find both the positive and negative coterminal angles of a given angle,θ, follow the procedures below. Thus, a coterminal angle calculator is a fun way to solve coterminal angle problems.

Coterminal angle calculator pi

Angles with the same initial and terminal sides are called coterminal angles. To find an angle that is coterminal to another, simply add or subtract any multiple of 360 degrees or 2 pi radians.

Coterminal angle calculator radians

If you’re working in radians, you will need to add or subtract a multiple of 2π to find the coterminal angles to your given angle. To determine whether the angles are coterminal, see if they agree with the coterminal angles formula provided in the article.

Coterminal angle calculator with solution

Example 1:

You can find coterminal angles for 60° and recheck them using the coterminal angles calculator.

Solution:

So, now, let us look at the solution to this problem.

Given angle = 60°

Positive coterminal angles of 60° are 60° + 360°, 60° + 720°, 60° + 1080°…

= 420°, 780°, 1140°…

Negative coterminal angles of 60° are 60° – 360°, 60° – 720°, 60° – 1080°…

= -330°, -660°, -1020°…

Example 2:

Find coterminal angles for -25° and verify them using the coterminal angles calculator.

Solution:

So, now, let us look at the solution to this problem.

Given angle = -25°

Positive coterminal angles of -25° are -25° + 360°, -25° + 720°, -25° + 1080°…

= 335°, 695°, 1055°…

Negative coterminal angles of 60° are -25° – 360°, -25° – 720°, -25° – 1080°…

= -385°, -745°, -1105° …

Similarly, you can try the coterminal angle calculator to find the coterminal angles for

Angle 45°

Angle -34°

Example 3:

Find the reference angle of 549°.

Solution:

So, now, let us look at the solution to this problem.

Let us find the coterminal angle of 549°. Thus, the coterminal angle is 549° − 360° = 189°.

Thus, we can see that the terminal side lies in the second quadrant. So, the reference angle is 180° -189° = -9°

Therefore, the reference angle of 549° is -9°.

Example 4:

Can you find the least positive coterminal angle of each of the following angles?

1. a) -80° b) -2500° c) 975°

Solution:

So, now, let us look at the solution to this problem.

We know that to find the coterminal angle we need to add or subtract multiples of 360°.

1. a) The given angle is – 80°

– 80° + 360° = 280°

Thus, 280° is the least positive coterminal angle of -80°.

1. b) The given angle is – 2500°

-2500 + 360° *7 = – 2500 +2520 = 20°

20° is the least positive coterminal angle of -2500°.

1. c) The given angle is 975°

975° – 360° * 3 = 975° – 1080° = 105°

30° is the least positive coterminal angle of 105°.

Answer: a) 280° b) 20° c) 105°.

Example 5:

Evaluate if π/4 and 5π/6 are coterminal.

Solution:

So, now, let us look at the solution to this problem.

Two angles are said to be coterminal if in any order their difference is a multiple of 2π.

π/4 − 5π/6

=−14π

=−7(2π), which is a multiple of 2π.

Thus, the given angles in the question are coterminal angles.

Answer: Yes, they are coterminal angles.

Example 6:

Evaluate if 675° and 1845° are coterminal.

Solution:

So, now, let us look at the answer to this question.

First, we will find the difference between the two angles.

675° – 1845° = -1170°. Clearly, 1170 is not a multiple of 360°

Hence, the given two angles are not coterminal angles.

Answer: No.

What are coterminal angles

We call the angles with the same initial side and the same terminal sides as coterminal angles. These angles are in the same place as the others, but their values are different.

Also, they share the same sides, are in the same quadrant and have the same vertices. Again, the terminal sides coincide at the same angle when the angles are rotated clockwise or anticlockwise.

Moreover, an angle is a measurement of a ray’s rotation around its origin. Also, the starting side of an angle is the position of the original ray. Again,  the terminal side is the position of the ray after we have rotated it.

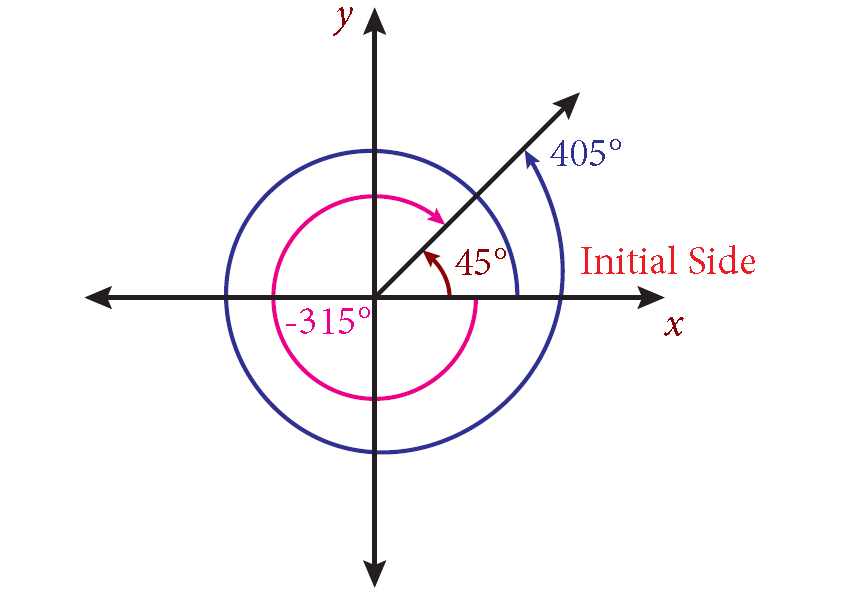
Consider 45 degrees. Because its terminal side is also in the first quadrant, its normal location is in the first quadrant. Now, let us carefully see the image below.

• 45° returns to its terminal side at 405° after a full anticlockwise rotation. In the first quadrant, 405° corresponds to 45°.
• 45° returns to its terminal side at -315° after a full clockwise rotation. In the first quadrant, -315° corresponds to 45°.
• Thus, 405° and -315° are coterminal angles of 45°.

Coterminal angles formula

The formula for determining the coterminal angles of an angle, whether in degrees or radians, is as follows:

• Degrees: θ ± 360n
• Radians: θ ± 2πn

θ ± 360n is a multiple of 360n in the preceding formula, where n is an integer and specifies the number of rotations around the coordinate plane.

Thus, as a result, 45°, -315°, 405°, – 675°, 765°, and so on are all coterminal angles. Only a few complete circles separate them. If the difference between two angles is a multiple of 360° (or 2π if the angle is in radians), they are said to be coterminal angles. Thus, we can conclude this. Let us now look at an example to help us understand the notion.

How to find coterminal angles

To find the coterminal angles, use the following formula:

• You can add or subtract multiples of 360° from the supplied angle if the angle is in degrees.
• If the angle is in radians, add or subtract multiples of 2π from the supplied angle.

To find the coterminal angles, we don’t need to use the coterminal angles formula. Hence, to get the coterminal angles of a given angle, we can either add or subtract multiples of 360° (or 2π) from it.

Positive and negative coterminal angles

Positive or negative coterminal angles are possible. Additionally, we have discovered that 390° and -690° are the coterminal angles of 30° in one of the previous situations.

Here,

• 390° is the positive coterminal angle of 30°.

And,

• -690° is the negative coterminal angle of 30°.

Thus, this results in θ ± 360 n, where n is positive while rotating anticlockwise and negative when rotating clockwise. To generate positive or negative coterminal angles, we determine whether to add or subtract θ ± 360 n(or 2π) multiples.

Coterminal angles and reference angles

We already know how to calculate a given angle’s coterminal angles. Thus, the angle between the angle’s terminal side and the x-axis is called the reference angle, and it is always between 0° and 90°. Moreover, the terminal side of the quadrant determines the reference angle.

The stages for determining an angle’s reference angle are determined by the quadrant of the terminal side:

• We start by determining the coterminal angle, which is between 0 and 360 degrees.
• The quadrant of the coterminal angle is then visible.
• The reference angle is the same as our specified angle if the terminal side is in the first quadrant (0° to 90°). If the specified angle is 25 degrees, the reference angle is also 25 degrees.
• The reference angle is (180° – provided angle) if the terminal side is in the second quadrant (90° to 180°). For example, if the specified angle is 100 degrees, the reference angle is 180 degrees – 100 degrees = 80 degrees.
• The reference angle is (given angle – 180°) if the terminal side is in the third quadrant (180° to 270°). For example, if the specified angle is 215 degrees, the reference angle is 215 degrees – 180 degrees = 35 degrees.
• The reference angle is (360° – provided angle) if the terminal side is in the fourth quadrant (270° to 360°). If the specified angle is 330 degrees, the reference angle is 360 degrees – 330 degrees = 30 degrees.

We can give the concept of reference angles in another way. Coterminal angles are the same as equal angles. Moreover, add or subtract 360 degrees (or 2π for radians) from the given angle to find its coterminal.

Thus, the reference angle is the smallest angle that can be formed by connecting the terminal side of an angle with the x-axis

Positive Coterminal Angles

We have mentioned below the concept of a positive coterminal angle.

To the given angle, multiply it by 360 degrees. The positive coterminal angles of θ will be θ + 360, θ + 720, etc.

Again, if the angle is supplied in radians, we multiply it by 2π to get the positive coterminal angles of θ.

Negative Coterminal Angles

We have mentioned below the concept of negative coterminal angle.

Subtract 360-degree multiples from the provided angle. The negative coterminal angles of θ will be θ- 360, θ – 720, and so on.

Then, we remove multiples of 2π from θ to determine the negative coterminal angles of θ when we represent it in radians.

Coterminal angles radians

Add and subtract 360° to find a positive and negative angle coterminal with a specified angle. If the angle is measured in degrees, or 2π if it is measured in radians.

How do you know if an angle is Coterminal?

We call the angles with the same initial and terminal sides coterminal angles. Finding coterminal angles is very simple. You can just as add or subtract 360° or 2π to each angle. It depends on whether the given angle is in degrees or radians.

How do you find a pair of Coterminal angles?

The coterminal angles are those that have the same initial and terminal sides. The coterminal angle of a given angle is calculated by adding or subtracting 360° or 2π to it.

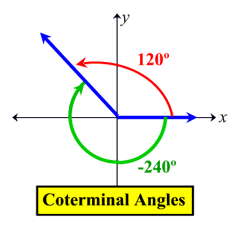
Coterminal angle pair

The coterminal angles of a given angle can be calculated by adding or subtracting a multiple of 360° or 2π radians. As a result, the coterminal of θ = θ + 360° × k if θ is given in degrees. If θ is given in radians, then, the coterminal of θ = θ + 2π × k.  If the difference between two given angles is a multiple of 360° or 2π, then we call them coterminal angles.

Coterminal angles in trigonometry

Angles with the same initial and terminal sides are called coterminal angles. Thus, depending on whether the given angle is in degrees or radians. It is as simple as adding or subtracting 360° or 2 to each angle to find coterminal angles. Also, there are an infinite number of coterminal angles to be discovered.

Coterminal angle FAQs

1.   What is the Procedure for Determining Coterminal Angles?

In order to find coterminal angles, we add or subtract multiples of 360° or 2π from the given angle, depending on whether it is in degrees or radians. However, we can represent some coterminal angles of 10° in different ways. Thus, for example, some coterminal angles of 10° can be 370°, -350°, 730°, -710°, and so on. Hence, in other words, the difference between the angle and its coterminal angle is always a multiple of 360°.

2.   What is the Coterminal Angle of 45°?

Let us find the coterminal angle of 45° by adding it to 360°.

So, 45° + 360° = 405°. Thus, 405° is the coterminal angle of 45°.

3.   What is the Coterminal Angle of

4.   -30° Between 0° and 360°?

If you want to find the coterminal angle of -30°, you have to add 360° to it.

So, − 30° + 360° = 330°. Thus, 330° is the required coterminal angle of -30°.

5.   How do you Find Positive Coterminal Angles?

To find positive coterminal angles, we can add a given angle by multiples of 360°. The positive coterminal angle of 120°, for example, is 120° + 360° = 480°.

6.   How do you Find Negative Coterminal Angles?

To find negative coterminal angles you need to subtract multiples of 360° from a given angle. So, for example, the negative coterminal angle of 100° is 100° – 360° = -260°.