Rationalization is a process that is used in elementary algebra. It is used to eliminate the irrational number in the denominator. There are numerous rationalisation techniques that can be used to rationalize the denominator. Making something more efficient is what the word rationalize literally means. Its use in mathematics entails reducing the equation to a more effective and simpler form.

The process of rationalisation is the removal of a radical. Also, an imaginary number from the denominator of an algebraic fraction.

That is, in a fraction, remove the radicals so that the denominator only contains a rational number. In this section, we will go over some key terms related to the concept of rationalisation.

We rationalize the denominator to make any calculation on the rational number easy.

So, when we rationalise the denominator in a fraction, we essentially remove any radical expressions from the denominator. Such as square and cube roots.

Thus, let us learn about rationalising the denominator. Let us also learn its meaning. And, how to do it with several examples in this article.

Thus, the rationalize the denominator calculator is a very helpful tool for solving sums.

Rationalize the denominator calculator

The rationalize the denominator calculator is a free online tool. It returns the rationalized denominator for a given input.

So, there are many online calculators on the internet. Thus, the online “rationalize the denominator calculator” tool speeds up and simplifies calculations. It displays the result in a fraction of a second.

Thus, the rationalize the denominator calculator is a very helpful tool for solving sums.

How to use rationalize the denominator calculator

The following is the procedure for rationalizing the denominator calculator:

In the 1st step: In the input field, enter the numerator and denominator values.

Step 2: To obtain the output, click the “Rationalize Denominator” button.

Finally, the end result will be displayed in the output field.

So, the rationalize the denominator calculator is a very useful tool for solving sums.

Rationalize the denominator calculator with solutions

Example 1: Justify the denominator in the given fraction: 1/√7.

Solution:

Hence, the answer is

Example 2: Rationalize the denominator in the provided fraction: 1/(5+√2)

Solution:

(7+√2) has a rationalizing factor of (7-√2). So, let us now multiply both the numerator and the denominator (7-√2).

Rationalize the denominator calculator with steps

Example 1: simplify

Solution:

To simplify this, do the following.

Example 2: Rationalize

Solution:

In the question, the denominator of the given fraction contains a binomial radical, 3+√10, which we need to rationalize.

Multiplying the numerator and denominator by the binomial radical’s conjugate i.e.,  3−√10,

     [ since (a² – b²) = (a + b) * (a – b)]

Dividing the numerator by -1, we get, −3 + √10

Thus, the answer to the question is −3 + √10

Moreover, you can also solve this using the rationalize the denominator calculator.

Rationalize the denominator with square roots

Example 1: Justify the denominator in the given fraction: 1/√11.

Solution:

Hence, the answer is

Example 2: Rationalize

Solution:

In the question, the denominator of the given fraction contains a binomial radical, 5+√7, which we need to rationalize.

Multiplying the numerator and denominator by the binomial radical’s conjugate i.e.,  5−√7,

     [ since (a² – b²) = (a + b) * (a – b)]

Thus, the answer to the question is .

What is rationalizing?

• Rationalizing is the process of multiplying one surd by another of the same kind to get a rational number. Thus, the rationalisation factor is the surd that is utilised to multiply (also known as RF).
• We need another √y: √y × √y = y to rationalize √y
• We need a rationalizing factor x -√y: (x +√y) × (x -√y) = (x)² – (√y)² = x² – y To rationalize x +√y
• Again, we can see that the rationalizing factor of 5√7 is √7: 5√7 × √7 = 5 × 7 = 35.

Rationalizing a surd

Surds are irrational numbers that, in their radical form, cannot be simplified any further. For instance, an irrational number √12 can be simplified further. It can be written as 2√3. But a number √2 cannot be simplified any more. As a result, the number √2 is a surd.

We can give a few examples of a monomial radical: √8, 2√2,

Also, a few examples of a binomial radical are √2 + √8, 1 – √3

Thus, the procedure for rationalising an expression is determined by whether the radical is monomial or binomial.

Moreover, the rationalize the denominator calculator is a very helpful tool for solving sums.

Rationalize the denominator meaning

Rationalizing the denominator is the process of transferring a root. Such as a cube root or a square root. We transfer it from the bottom to the top of a fraction (denominator and numerator). However, in this approach, the fraction is reduced to its simplest form, and the denominator becomes rational.

Rational denominator	Irrational denominator
√3/3	1/√5
5√6/6	5/√6
(3√7+7)/7	(3√7+7)/√7

Thus, the above-given table lists the irrational denominators and their equivalent rational values.

Standard Form

The standard form to represent the rationalization of a denominator is given as follows:

So, let us consider a fractional number, 1/(a-√b)

Hence, the rationalized form of the number is written as

[1/(a-√b)] × [(a+√b) / (a+√b)]

Rationalized Form= [(a+√b) / (a2 -b)]

Rationalize the denominator and simplify

Step 1: To remove the radical from the denominator, multiply the numerator and denominator by a radical.

Suppose the radical in the denominator is a square root. So, multiply it by a square root. Note that, when multiplied by the denominator, it produces a perfect square.

However, if the radical in the denominator is a cube root, multiply by a cube root. Do this to get a perfect cube under the radical when multiplied by the denominator. Then, continue with this process.

Read Also: Double Integral Calculator: Definition, Examples

Moreover, it is worth noting that the phrase “perfect square” implies that you can calculate the square root of it. Similarly, “perfect cube” implies that we can take the cube root of the number, and so on.

So, remember that the fractions will be equivalent if you multiply the numerator and denominator by the same thing.

Step 2: Ensure that all radicals have been simplified.

However, some radicals will already be simplified, but make sure to simplify any that aren’t.

Step 3: If necessary, simplify the fraction.

But, take care of a thing. A factor on the outside of a radical cannot be cancelled out by a factor on the inside of the radical. So, to cancel out common factors, they must both be inside the same radical or both be outside the radical.

However, you can try the rationalize the denominator calculator. The rationalize the denominator calculator is a very helpful tool for solving sums.

Rationalize the denominator using conjugates

Now, we must first understand conjugates before learning how to rationalize a denominator. A conjugate is a surd that is comparable to a surd but has a different sign. (7 + √5) has a conjugate of (7 – √5). Thus, the conjugate is the rationalizing factor in the process of rationalising a denominator.

Hence, let us look at the following procedure for rationalising the denominator with its conjugate.

• In the 1st step: Multiply the numerator and denominator by a conjugate that removes the radicals in the denominator.
• Step 2: Verify that all of the surds in the specified fraction are in their simplest form.
• Finally, we can now simplify the fraction even more if necessary.

Moreover, to better comprehend this notion, consider rationalizing the denominator of the fraction 1/(7+√5).

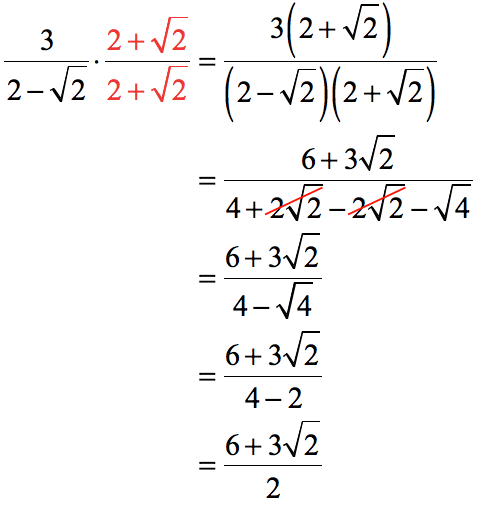
Rationalize the denominator using algebraic identities

Algebraic identities are another technique to justify the denominator.

(a² – b²) = (a + b) * (a – b) is the algebraic formula that is  used in the rationalisation process.

• Thus, for rationalizing (√a -√b), the rationalizing factor is (√a +√b).
• Again, for rationalizing (√a + √b), the rationalizing factor is (√a − √b).
• (√a − √b) × (√a + √b) = (√a)² – (√b)² = (a – b)

Moreover, to better comprehend this notion, consider rationalising the denominator of the fraction 4/(√11-√5).

Rationalize the denominator with 3 terms

We can use the same steps we used to rationalize the denominator with two terms, but with a slight variation.

Thus, consider a denominator with the following three terms: a + b + c. So, by multiplying with its conjugate, a – b, we rationalized a denominator with two terms: a + b. We can use the same logic to rationalize a denominator with three terms. Do this by grouping them as a + b + c = (a + b) + c. We have the following using the difference of squares formula: [(a + b) + c] × [(a + b) – c] = (a + b)² − c².

Let us now look at this example.

So, now, we can multiply the numerator and denominator with the conjugate of (2√3-1), which is (2√3+1).

Rationalize the denominator calculator FAQs

1.   How do you Rationalize a Denominator with two terms?

Here are the steps to rationalize the denominator with two terms:

• To rationalize the denominator with two terms, multiply the fraction’s numerator and denominator by the denominator’s conjugate.
• Next, to find the conjugate of two terms, we must first change the sign of the terms.
• Again, combine all terms that are similar and simplify the radicals.
• However, if possible, try to reduce the fraction to its simplest form.

2.   How do you rationalize the denominator of 1/(2+√3)?

Let us rationalize the denominator of the given fraction 1/(2+√3). We do it by multiplying the conjugate by both the numerator and the denominator (2 – √3).

3.   How do you rationalize a denominator with three terms?

We can use the same steps we used to rationalize the denominator with two terms, but with a slight variation. So, consider a denominator with the following three terms: a + b + c.

Now, we have to multiply it with its conjugate, a – b, we rationalized a denominator with two terms: a + b. Thus, we can use the same logic to rationalize a denominator with three terms. We do it by assembling them as a + b + c = (a + b) + c.

So, the difference of squares formula gives us: [(a + b) + c] [(a + b) – c] = (a + b)² + c².

4.   How do you rationalize a denominator of 1/√7?

Another √7 is required to rationalize √7 in the denominator.

Thus, as a result, the answer is √7/7.

Therefore, the answer to the question is √7/7.

5.   How do you rationalize a denominator that contains a square root?

To rationalize a denominator, multiply both the numerator and the denominator by the same square root. To rationalize the denominator 1/√5, for example, multiply the numerator and denominator by √5.

Let us look at an example.

6.   What Is Rationalize the Denominator meaning?

Rationalizing the denominator refers to the process of moving a root. Such as, a cube root or a square root. It is removed from the bottom to the top of a fraction. In this manner, we reduce the fraction to its simplest form, and the denominator becomes rational.

7.   What exactly are surds?

A fraction is made up of two parts. The first is the numerator, and the second is the denominator. Surd is a number that cannot be simplified further, such as the square root or cube root. Surd can be either a numerator or a denominator.

8.   How can the square root be used to rationalize the denominator?

To rationalize the denominator, multiply and divide the given fraction by the same square root value. The denominator will be a rational number as a result.

9.   How can the denominator with two terms be rationalized?

Find the conjugate of the denominator to rationalize the denominator with two terms. The fraction is then multiplied and divided by the denominator’s conjugate.

10.  Why Do We Justify Surds?

We rationalize the surds or radicals in a fraction’s denominator in order to make the denominator a rational number. To do so, we usually multiply both the numerator and the denominator by a suitable radical and simplify.

11. What Are the Rationalization Rules?

When rationalizing a denominator, the following rules can be followed:

Check to see if all of the radicals or surds have been simplified.

Find the appropriate radical and multiply it in the numerator and denominator to remove the radicals from the denominator.

12. What Is the Rationalization Method for Radicals in Denominators?

The radical in the denominator of a fraction can be rationalized as follows:

In the first step: Multiply the numerator and denominator by a radical that removes the radicals from the denominator.

Step 2: Ensure that all radicals are in their simplest form.

Finally, simplify the fraction even more if necessary.

13. What Is the Purpose of Rationalizing Denominators?

Suppose the denominator is linear in terms of a radical. Both the numerator and the denominator are multiplied with a value. The value expands and rationalizes the denominator’s product. Consider the denominator with a radical expression of the form x + √y or x + i√y. The fraction must be multiplied by the conjugate of the expression i.e., x – √y or x – i√y.