In this article, we will know in detail about tangential velocity, its formula and derivation, and the application of it.
Tangential velocity meaning
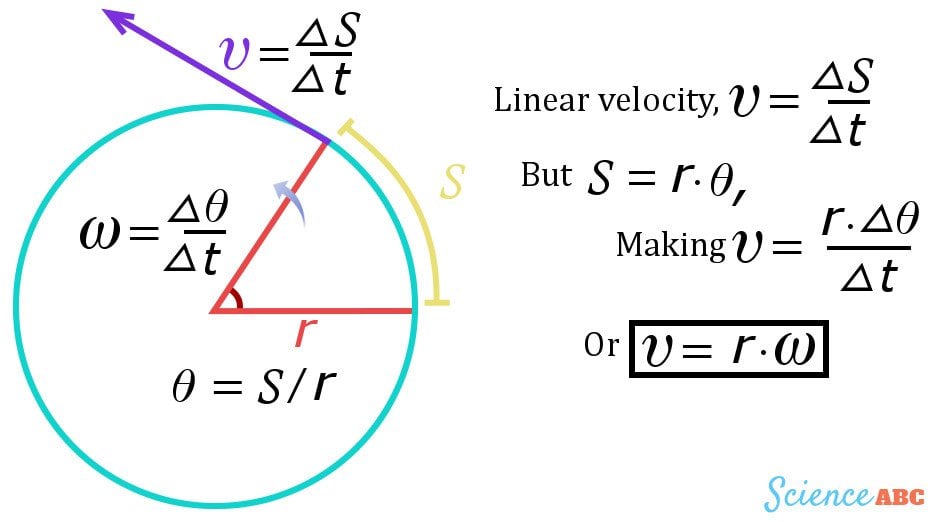
Jumping off a cliff straight into the ocean is dangerous. Although the decision to make the jump creates a sense of thrill. Remember standing on the edge of a merry-go-round and feeling a force trying to pull you away and out of it. Although at that time it felt a bit magical, now we do know that there is a force behind it. This very force represents the tangential velocity.
Tangential velocity is the part of motion along the edge of a circle measured at any instant. It describes the motion of an object along the edge of this circle. Moreover, the direction at any given point on the circle is always along the tangent to that point.
If we ever need to explain tangential velocity in simple terms, we can say that the it represents a point tangent to a rotating wheel. Therefore, angular velocity, ω, and tangential velocity, Vt , can be considered inter-related through the formula: Vt = ω r.
Read Also:Combine Like Terms Calculator: Steps, Examples, rules and more
Here, r is the radius of the the circle on which we will measure the tangent. Needless to say, tangential velocity represents the motion measured at any point of a circle at any instant in time. As the name suggests, tangential velocity, also known as the motion of a circular object along its edge of it. In addition, the direction at any given point on the wheel is always along the tangent to that point.
Tangential velocity- what is a tangent?
A tangent simply stands as a line that touches a circle at only a single point. Talking about the graph, tangential velocity is a non-linear curve. The relationship between the “x” and “y” coordinates on the two-dimensional graph showcases the equation.
When we think of a curve the first thing that pops into our mind is a circle. Not only that, but a circle must be also represented by an equation with the main component r. This means that for a constant radius ‘r’, coordinates x and y trace out a perfect arc. Moreover, with time the arc completes a revolution and meets the starting point. This exactly looks like a snake eating its own tail.
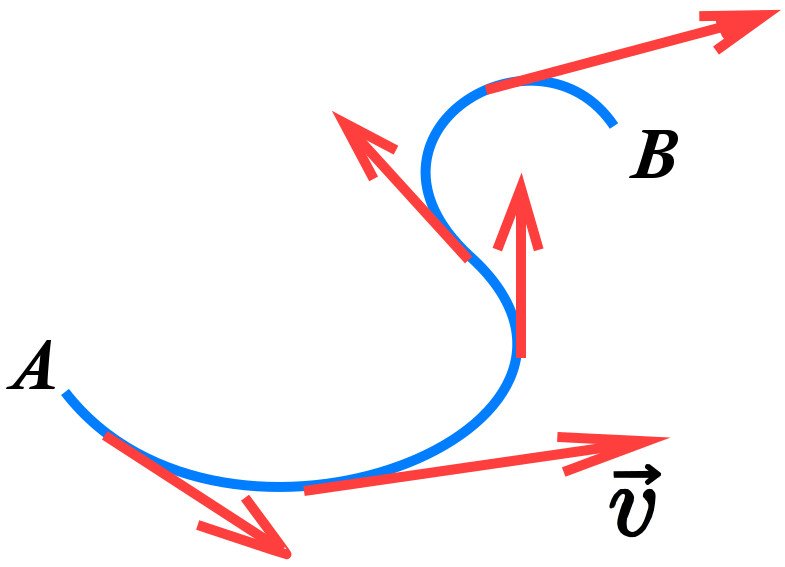
As already mentioned above, tangential velocity represents the motion of an object at the edge of this circle. Moreover, the direction will always be along the tangent on that point of the circle at any instant in time. Although we are talking about uniform motion right now, the theory does not limit itself to just uniform circular motion. It works perfectly with any kind of non-linear motion. Suppose a circle is moving non uniformly and we make a point; traveling from point A to point B. In this case, we will represent the trajectory of the this velocity at different times through red dots.
Tangential velocity formula
Firstly, in order to derive the velocity formula, we require displacement. Same here, for the tangential velocity we need to calculate the angular displacement, ‘q’. To do that, we need to find the ratio of the length of the arc ‘s’. An object traces the arc s on a circle due to radius ‘r’. It stands as the angular portion under the arc.
Moreover, it stays between the two lines originating from the center and connected to its ends. The SI unit measured in radians. The rate of change of the angular displacement of any body is known as angular velocity. It is denoted by ‘w’. The standard unit is radians/second (rad/s). It is not the same as linear velocity,since it only deals with objects moving in a circular motion. It measures the rate at which angular displacement is swept.
The linear component of angular velocity is known as linear velocity. It is the rate of change of linear displacement of an object. Linear displacement can also be written as the length of the arc. The rate of change of the product of radius and angular displacement ‘q’ is the linear velocity of an object. We do’t include the radius in the operation because it is a constant. Therefore, we find that the velocity is the product of the object’s angular velocity and the radius of the circle.
Tangential velocity derivation
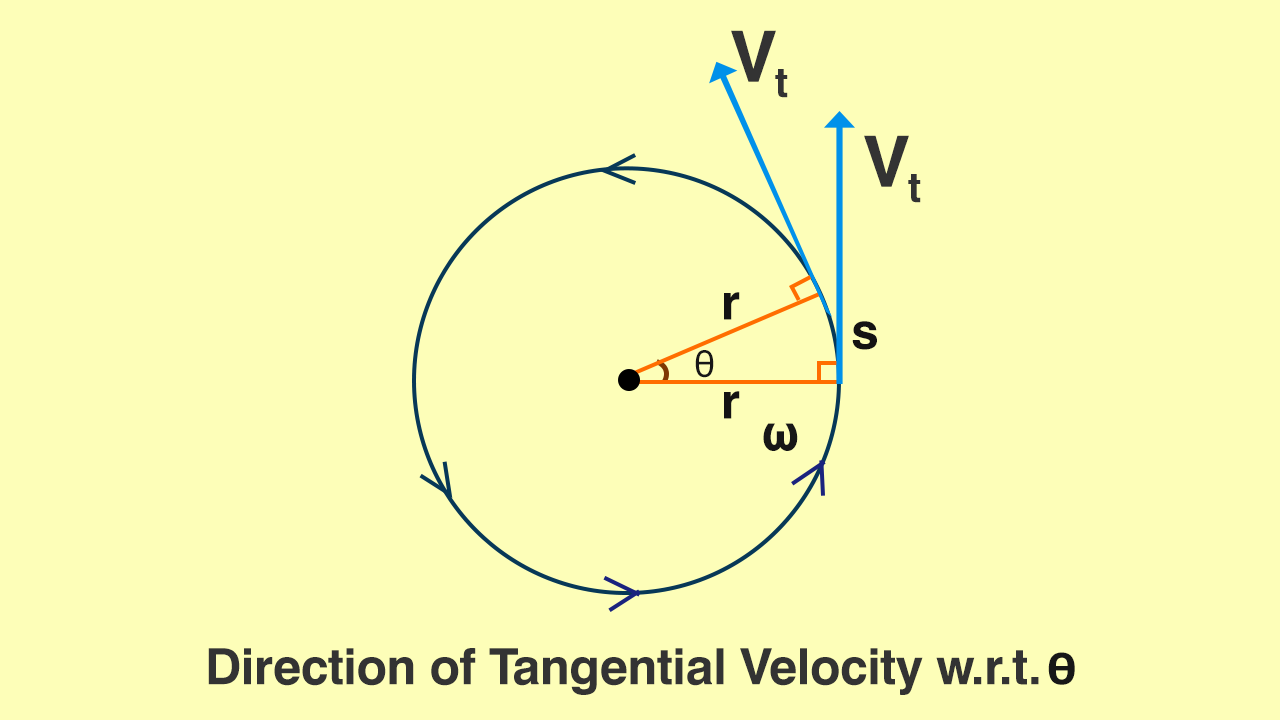
We can also say that tangential velocity is just linear velocity in a circle. Not only that but we can also define linear velocity in terms of the time period. The velocity can be called ‘s/t’ (distance/time) if the time required to travel once around the circle is t. The reciprocal of ‘T’ is known as frequency and we denote it as ‘f’. The product 2pf is known as angular frequency and is denoted by ‘w’ . As a result, it helps us arrive at the previously derived result.
V=S/T
=(2 r)/T
=2 f r
V=ωr
Here, S= length of the arc
T= time period
R= radius
ω=angular frequency
V=tangential velocity
Tangential velocity and average velocity difference
The angular displacement covered by an object in unit time is called angular velocity. On the other hand, tangential velocity is the velocity, which is tangent to the circular path.
Tangential velocity vector
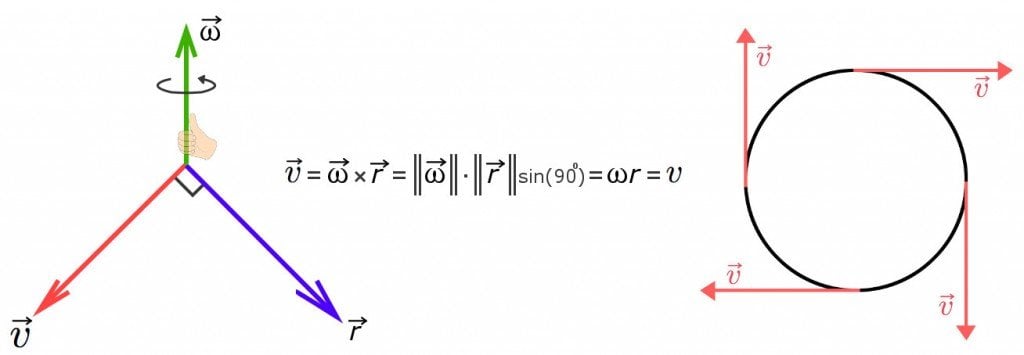
Needless to say, tangential velocity works as a vector. In other words, it has both size and direction. Vectors are represented by putting an arrow above the standard symbol. Even though the direction continuously varies, the total sum or resultant vector remains the same. Every vector can be represented as the cross or sum of two vectors, or say the multiplication of their magnitudes keeping the angle of sine between them in mind. The resultant vector must and always should be perpendicular to the vectors.
Nonetheless, the value of tangential velocity shows no change to the change in direction & tangential velocities with the same magnitude but different directions on arbitrary edges of a circle.
The two vectors whose product gives the tangential velocity are the radius ‘r’ and angular velocity ‘w’. Moreover, the right-hand rule says that if you imagine your right hand as the axis and then just curl your fingers in the direction of the motion of the body, your thumb will point towards angular velocity. This theory clearly implies that these two forces are perpendicular to each other.
Not only that, but since the sine of 90 is one, the resultant vector of these quantities at any point on the circle will always remain the same. Not only that, but the objects inside or on the circle carry the same angular velocity, although have different tangential velocities. This happens since the motion depends on the radius, as we can see in its formula. As a result, people standing at the rim of a merry-go-round tend to fly off at greater velocities than those who stand close to the center.
Tangential velocity of a satellite
We can find tangential velocity everywhere around us. This does not limit to just linear motion. Instead, it works for any nonlinear motion. Non-linear motion can be anything, whether you see a sudden jump from a swing or the deviation of a satellite from its orbit. The Earth itself from its circular orbit represents a perfect example of tangential velocity. However, the trajectory of a satellite is not completely circular.
This motion usually occurs in an elliptical pattern where the centripetal force pulls it inward and the linear velocity pushes it straight forward. Talking about real-life examples, the ISS has an average velocity of 7.66 km/sec in the tangential orbit. When a satellite revolves around the earth, the gravity of the earth attracts it. This force constantly pulls the satellite toward the center of the earth. In short, this pull works as a centripetal force and causes centripetal acceleration.
Tangential velocity FAQs
1. What is meant by tangential velocity?
Tangential velocity represents the linear speed of an object which follows a circular trajectory. As a result, the point located on the outer edge of a merry-go-round covers a greater distance in one complete rotation when we compare it to the center.
2. How do you calculate tangential velocity?
To find the tangential velocity, we need to divide the circumference by the amount of time it takes to complete one rotation. This will give us the tangential speed. For instance, if we have an object which takes 6 seconds to complete one rotation. Just divide 18.84 by 6 and you will find the tangential velocity equals 3.14 feet per second.
3. What is tangential in physics?
Tangential velocity is an important part of physics. It stands as a force that works on a moving body in the direction of a tangent in the circular path of the body while in motion.
4. Is tangential speed a vector?
Yes, tangential velocity represents a vector in which the magnitude is the speed. Moreover, speed represents distance divided by time. For tangential velocity, we express it as the motion along the corner of a circle. Moreover, the direction of the vector at any given point on the circle runs along the tangent line.
5. How do you find tangential velocity from radial velocity?
For an object that follows a circular trajectory, it carries a speed that is directly proportional to the distance from the axis on which it rotates. Talking as per the given equations, the tangential velocity is calculated when we multiply the distance by the angular velocity(in radians/sec).
6. Where is tangential velocity greatest?
When we measure the tangential from the low point, the position changes up to a maximum. Along with that, the amplitude of the motion also changes. The tangential velocity hits zero when it hits the highest point and greatest at the lowest point.
7. What is the relationship between tangential and rotational velocity?
Angular acceleration represents the change in angular velocity divided by time. While on the other hand, the tangential acceleration represents the change in linear velocity divided by time. although we must keep in mind that angular acceleration has no effect when we change the radius. Although, tangential acceleration does.
8. Is tangential velocity the same as linear velocity?
No, they are not the same. While linear velocity represents the speed coming toward us or going away from us, tangential velocity. On the other hand, Tangential velocity works around our field of view. With these points in our mind, we can set up a vector rectangle, with the linear velocity being diagonal.
9. Where is the direction of tangential velocity?
The tangential velocity vector always stays perpendicular to the radius of the circular path along which the object moves. The tangential velocity vector always stays at an acute angle to the radius of the circular trajectory on which the object revolves.
10. What’s the difference between tangential and angular speed?
Angular speed is the rate of change of the angle (in radians) with time. Moreover, it has units 1/s. On the other hand, tangential speed represents the speed of a point on the edge of the revolving circle. we can also derive it as the angular speed multiplied by the distance from the axis point.
11. Is tangential velocity constant?
The tangential speed is constant, yes. But the direction of the tangential velocity changes from time to time being a vector. Moreover, the direction of the centripetal acceleration always pushes inwards along the radius vector of the circular motion.
12. How do you find tangential velocity with centripetal acceleration?
aT=d|→v|dt shows the basic known formula to find the tangential velocity. The direction of tangential acceleration is tangent to the circle. While the direction of centripetal acceleration is radially inward toward the center of the circle.
13. What are radial and tangential velocity?
When an object revolves, it has angular or linear velocity. However, at any single instant of time, the motion steps out of the circular trajectory. In this case, the direction gets tangent to its circle of motion. This represents the tangential velocity.
14. What are tangential and normal acceleration?
The tangential acceleration is the measure of the rate of change in the magnitude of the velocity vector, or say speed. Moreover, the normal acceleration represents the measure of the rate of change in the velocity vector.




