Geometric shapes are something that we come across in our primary classes. We get to know the various geometric shapes in math right at the beginning of our middle-school days. So, the geometric shapes that we know mostly belong to three dimensions. However, out of these, the only 1-D geometric shape that we know is a straight line. 2-D geometric shapes are the ones that we know the best about. So, the triangle, the square, the rectangle, the circle, the parallelogram, the rhombus, the hexagon, the heptagon, the octagon, the nonagon, the decagon, and so on till infinity all come under 2-D shapes. Moreover, we also find 3-D geometric shapes. So, in this case, there is the cube, the cuboid, the sphere, the cylinder, the cone, and so on.
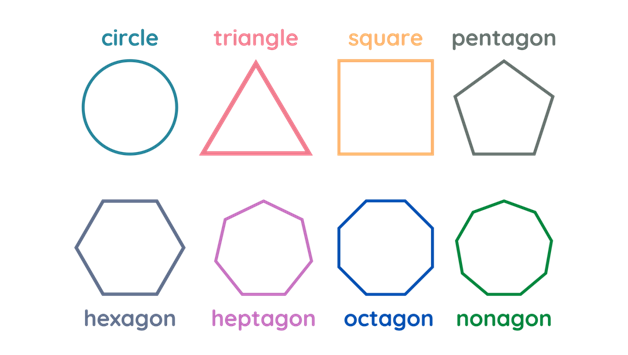
However, if you think, you will realize that the 1-D or 2-D shapes hardly find much relevance in the real world. So, this is because the world that we live in is 3-D. However, let us understand the concept better with the definition and examples.
Geometric shapes definition with examples
So, it is very difficult to understand the concept or definition of geometric shapes without examples. This will allow you to write on paper the shapes that you have at hand. Moreover, the expanse of geometric shapes is huge. So, a general definition cannot cater to every kind of geometric shape. However, let us see what geometric shapes mean at first.
Geometric shapes meaning
So, geometrical shapes are the diagrams that we use to present the forms of various objects. Now we are already aware of the fact that these figures can be either two-dimensional or three-dimensional. So, now, the two-dimensional figures lie on the x-axis and y-axis only. The name 2-D itself suggests that there will be 2 dimensions or axes. Similarly, 3-D will have 3 dimensions or axes. So, these are the x, y, and z axes. Therefore, the z-axis is the extra one in 3-D figures. It represents the height of the figure. Moreover, you can also refer to the 2-D figures as flat shapes or closed shapes.

Moreover, geometric shapes can be broadly categorized into 2 divisions. So, the first kind is that they may be regular or symmetrical. Therefore, this means that all the sides in this shape are either equal or they have a fixed ratio. However, the second kind is when they are asymmetrical or irregular. In this case, the lines forming the geometric shape have no restraint. Therefore, mathematicians sometimes call them organic shapes as well.
Read Also:Combination Formula: Definition, Examples & more
However, no matter what figure you want to draw, you have to begin with a line, a line segment, or a curve. So, by connecting these segments, we can have different types of shapes and figures. For example, a triangle has the connection of three-line segments while a pentagon is made of five-line segments, and so on. It matters how many lines you are using and how you arrange them. However, it is also important to remember that not every figure is a complete figure.
Geometric shapes examples
So, let us first begin with what open and closed shapes are. Therefore, for drawing an open shape you need to have a separate initial and ending point that cannot coincide under any circumstance. So, your line has to be a regular, or an irregular, a straight, or a curved line that does not enclose any space. However, if the initial and endpoints coincide, the shape contains within it a space. Therefore, these are closed shapes. Circles, squares, rectangles, and all that we generally talk about are closed shapes. So, let us take a quick look at their properties and formulas now.

Geometric shapes and their properties
Therefore, as we already know, the expanse of geometric shapes is large. So, each of the figures that fall under it has its own set of properties because no two shapes are the same. However, it is important to realize that when you state general properties, you can only do that for the regular geometric shapes. So, it is impossible to define irregular shapes by any of their properties because they have no set pattern.
Geometric shapes triangle
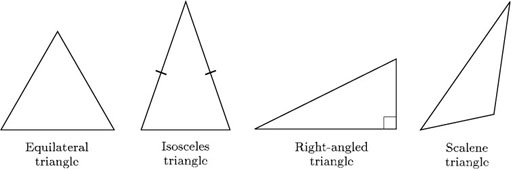
Triangles are a type of 2-D geometric shape. Hence, it is a polygon with three sides. It also has three edges and three vertices. However, the most important part of a triangle that you must know is that the sum of their internal angles must be equal to 180 degrees.
Geometric shapes squares
Squares are probably the first geometric shapes that we ever encounter. So, they are 2-D shapes that have four sides. Moreover, all four of them are of the exact same length. Additionally, all the angles are equal to cutting the sides at perfect 90 degrees.

Geometric shapes rectangle
So, quadrilaterals are 2-D shapes that have four sides like squares and rectangles. This comes from Quadri meaning 4 and lateral meaning lines. Therefore, four lines join with each other to form these geometric shapes. Hence, a rectangle also has 4 sides with vertices at 90 degrees. However, it is not the same as a square. This is because unlike in a square, only the opposite sides are equal in a rectangle.

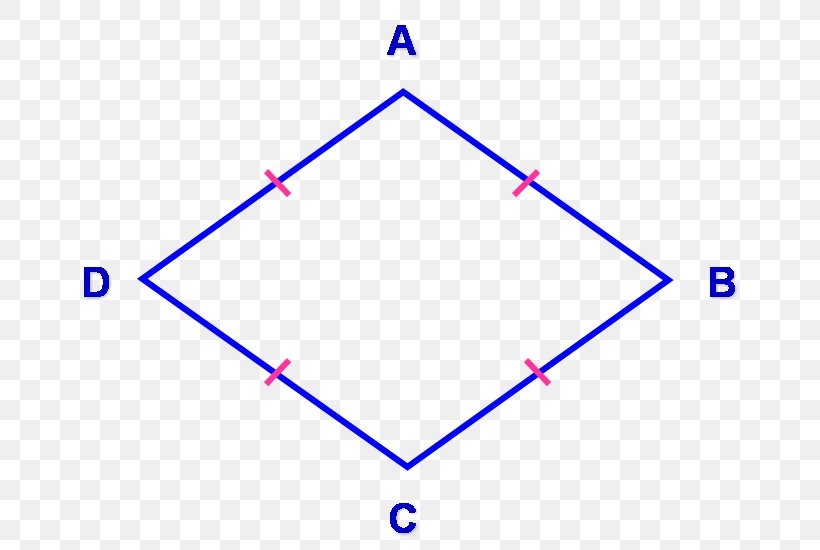
Geometric shapes rhombus
So, these are again 2-D geometric shapes that you can call a square without having compulsory 90-degree vertices. Therefore, it is also a quadrilateral. So, it is a parallelogram but the sides are all equal. Now, parallelograms are quadrilaterals that have two pairs of parallel sides. Moreover, their opposite angles are also the exact same. Therefore, in short, a rhombus has all the sides and opposite angles equal but the angles are not all 90 degrees.
Geometric shapes circle
So, in a circle, the locus of all points are at a fixed distance from a reference central point. Now, this central point is what we call the center of the circle. Moreover, the movement of the loci creates its circumference. So, the radius is the fixed distance between the center of a circle and a locus. Moreover, the diameter is the distance between two opposite loci touching the center. Circles are also 2-D shapes.

Geometric shapes cube
So, cubes are 3-D geometric shapes having all sides equal to each other. Therefore, a cube has 6 faces, 8 vertices, and 12 edges. Moreover, all the sides are equal in size. Therefore, each face of a cube becomes a square.

Geometric shapes cuboid
These are 3-D geometric shapes with 6 faces, 8 vertices, and 12 edges. However, they are not the same as cubes. The primary cause behind this is that each face of a cuboid is a rectangle. So, the length, breadth, and height are not the exact same but all opposite sides are equal.
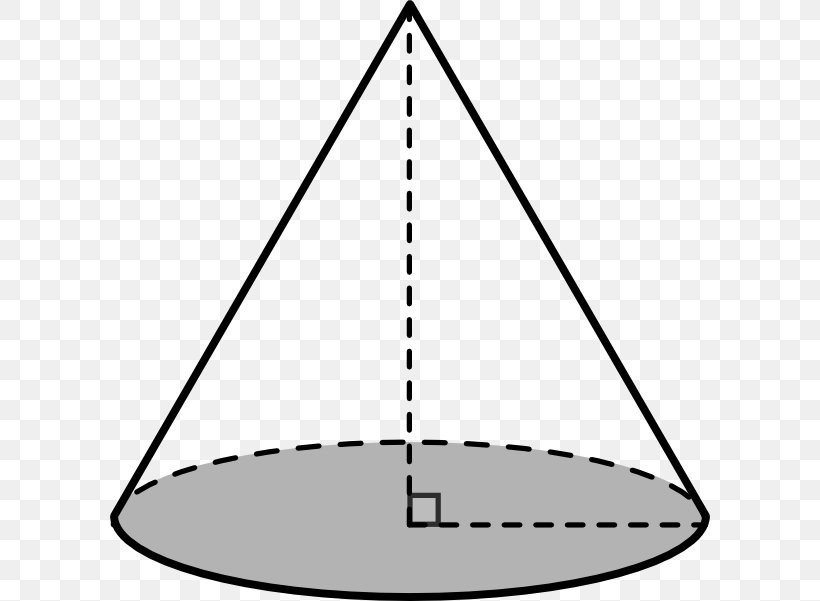
Geometric shapes cone
So, all of us know about ice-cream cones. These are what we all call cones in geometric shapes. So, they are 3-D with a circular base. Moreover, the sides narrow down from the base to the top like a triangle. Therefore, there is a point at the top. So, this becomes the apex or the vertex.

Geometric shapes cylinder
The interesting part about cylinders is that they are 3-D geometric shapes without a vertex. Hence, they have two parallel circular bases. Moreover, these two bases find connections via a curved surface.

Geometric shapes polygon
So, these are geometric shapes with only line segments and no curves. They might be various closed figures depending on different lengths of sides and angles. Hence, geometric shapes like squares, rectangles, hexagons, octagons, pentagons, heptagons, and so on are all polygons.
Now, let us take a look at the formulae of some of them.
Geometric shapes and their formulas
So, there are some basic formulas for geometric shapes. However, the formulae differ from the geometric shapes:
The perimeter of a square = 4a, where a is each side.
Moreover, the perimeter of a rectangle = 2 x (l + b), where l is the length and b the breadth.
Now, let us see the perimeter of a triangle = a + b + c, where a, b, and c are the three sides of the triangle. Therefore, if all these sides are the same, the triangle is equilateral. So, if two sides are equal, the triangle is isosceles. Finally, if no side is equal, the triangle is scalene.
So moving on we have the circle. Since it is not a line we do not say the perimeter of a circle but we say its circumference. The formula for finding this is 2 𝞹 r where r is the radius of the circle.
Geometric shapes and area formulas
Therefore, let us begin with the 2-D geometric figures first.
So, the area of a square is a^2 where a is each side of these geometric shapes. Similarly, the area of a rectangle is l x b where l and b are respectively its length and breadth. Then, we have the area of a triangle which is ½ x b x h. So, here b is the base and h is the height of the triangle. However, the height of the triangle might not be always available. Moreover, if you have a scalene triangle, the Pythagorean theorem makes no sense. Therefore, in those cases, you have to first find its semiperimeter and then apply Heron’s formula.
Finally, to find the area of the circle, the formula that you need is 𝞹 r^2. So, here r is the radius of the circle.
Geometric shapes surface area
For a cube, the surface area is 6 a^2, where a is the length of each side. So next, for a cuboid, the surface area is 2 ( l x b + b x h + l x h), where l, b, and h are respectively the length, breadth, and height of the cuboid. Moreover, the surface area of a sphere is 4𝞹 r2, where r is the radius of the sphere. So now there are the cylinder and the cone. However, for both of these geometric shapes, there can be a total and a curved surface area. So, while the total surface area considers only the sides, the curved surface area considers both bases and sides.
Therefore, the curved surface area of a cylinder is 2 𝞹 rh, and the total surface area is 2𝞹r (r + h). So, here r is the radius of the base, and “h” is the height of the cylinder. The curved surface area of a cone is 𝞹rl and the total surface area is 𝞹r (r + l). So, here r is the radius of the base and l is the length of each side. Moreover, you can find out the value of l from h and r by applying the Pythagoras theorem.
Geometric shapes volume formulas
So, 2-D geometric shapes cannot have volume formulas because they occupy only one plane. So, they have an area but not a volume. However 3-D shapes have volume formulas because they occupy a space in all three dimensions.
Therefore, the volume of a cube is a^3 where a is the length of each side of the cube. The volume of the cuboid is also similar but we write it as l x b x h where l, b, and h are respectively the length, breadth, and height of the cuboid because for a cuboid all of these are different. The volume of a sphere is 4/3 𝞹 r^3 where r is the radius of the sphere. Moreover, the volume of a cone is ⅓ 𝞹 r^h where r and h respectively are the radius of the base and the height. Finally, the volume of a cylinder is 𝞹 r^h where r and h respectively are the radius of the base and the height.
Geometric shapes edges vertices faces
So, let us see what each of these terms means with respect to geometric shapes.
Therefore, edges in geometric shapes are a particular type of line segment joining two vertices in a polygon, polyhedron, or any higher-dimensional polytope. Moreover, if you consider a polygon, an edge is a line segment on the boundary. Therefore, we often call it a polygon side.
Read Also:Coterminal angle calculator — everything you need to know about this
So, the next thing that we need to know is vertices. Vertices are the plural of a vertex. So, these are the corners of the geometric shapes. So, a vertex is where two lines or edges in any polygon meet.
Therefore, faces in solid geometry are flat surfaces or planar regions. Hence the boundary of any solid object is built by faces. So, a polyhedron is formed when faces bind a 3-D solid.

Geometric shapes characteristics
So, we can note down and summarize some of the basic characteristics of geometric shapes-
- Geometric shapes can have any and every kind of structure.
- Every structure has some properties unique to it alone. However, in some cases, structures might have the same properties as squares have all the properties of rectangles but not the other way around.
- They can be either open or closed.
- The lines and points that form them define their properties.
Geometric shape FAQs
What makes a geometric shape geometric?
Ans. This is a very valid question because how do we know which shapes are geometric shapes? So, a geometric shape is a piece of geometric information that remains when location, scale, orientation, and reflection are removed from the description of a geometric object.
What is the importance of geometric shapes?
Ans. So, they are key in defining something as you want it to be. Let us say you need to buy a cupboard, you will need its dimensions. However, the most important use is perhaps architecture and civil engineering- from the shape of an engine to the shape of the ventilators in your home. Moreover, we also need geometric shapes for measuring an area, a piece of cloth- literally everything.
Are geometric shape 2d and 3d?
Ans. So, as we already know, geometric shapes can be both 2-d as well as 3-d depending on the kind of figure that we are considering. 2-d shapes are planar and hence they only occupy an area. However, 3-d shapes have three dimensions and can occupy a volume in the space.
Who invented geometric shape?
Ans. Euclid is the father of most geometric shapes. Moreover, he was one of the greatest mathematicians ever. Mathematicians consider him the father of geometry.
Is a star a geometric shape?
Ans. Yes. Any 2-D closed shape with lines is a polygon. Therefore, a star is a regular polygon. So, it is a geometric shape.
Is a square a geometric shape?
Ans. Yes, just like a star, the square is also a regular polygon. Therefore, it is a geometric shape.
What are triangle angles?
Ans. So, a triangle has three sides and three vertices. Therefore, three vertices would mean three angles, each between two sides. However, for triangles, these angles are important. If all three angles are equal, the opposite lines will also be equal thereby making the triangle equilateral. If two are equal, the triangle becomes isosceles. Moreover, if none are equal, the triangle becomes scalene.




